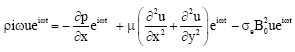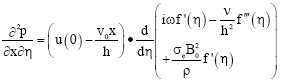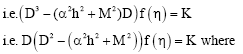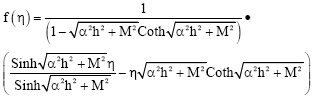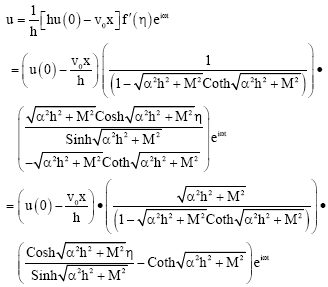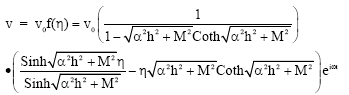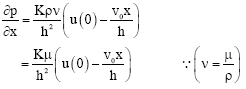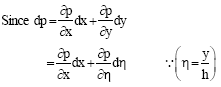Research Article
Unsteady Magnetohydrodynamic Stokes Flow of Viscous Fluid Between Two Parallel Porous Plates
Department of Mathematics, Sathyabama Institute of Science and Technology, Deemed University, Old Mamallapuram Road, Chennai-600 1 1 9, India
S. Krishnambal
Department of Mathematics, Anna University Chennai-600 (325), India