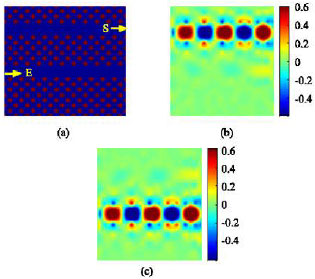
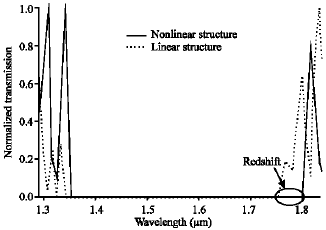
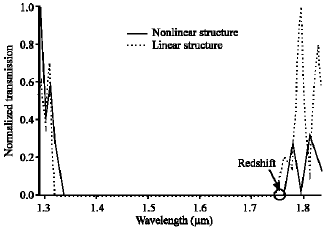
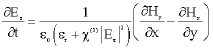Research Article
A Novel All-Optical Switch Based on a Photonic Crystal Coupler
Telecommunications and Digital Signal Processing Laboratory, Institute of Electronic, University Djillali Liabes of Sidi-Bel-Abbes, Sidi-Bel-Abbes 22000, Algeria
R. Naoum
Telecommunications and Digital Signal Processing Laboratory, Institute of Electronic, University Djillali Liabes of Sidi-Bel-Abbes, Sidi-Bel-Abbes 22000, Algeria