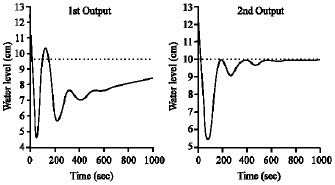
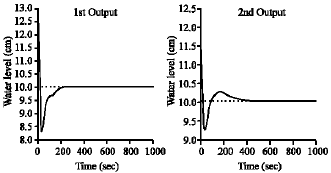
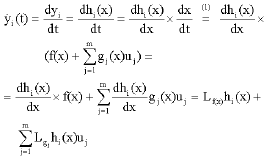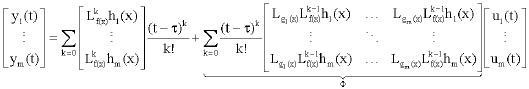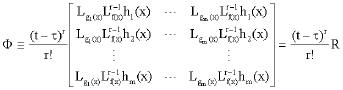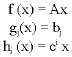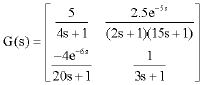Research Article
Input-Output Pairing for Nonlinear Multivariable Systems
Department of Electrical and Electronic Engineering, K.N. Toosi University of Technology, Tehran, Iran
Ali Khaki-Sedigh
Department of Electrical and Electronic Engineering, K.N. Toosi University of Technology, Tehran, Iran