Research Article
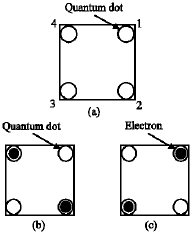
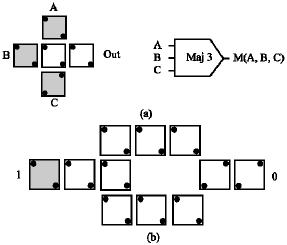
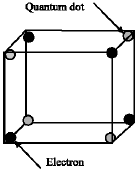
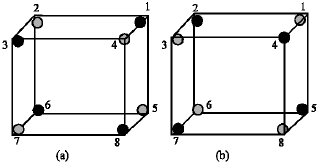
A Novel Design for Quantum-dot Cellular Automata Cells and Full Adders
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran
Omid Kavehei
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran
Keivan Navi
Department of Electrical and Computer Engineering, Shahid Beheshti University, Tehran, Iran