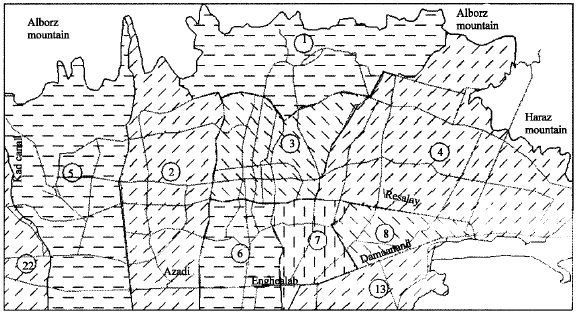
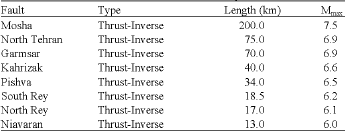
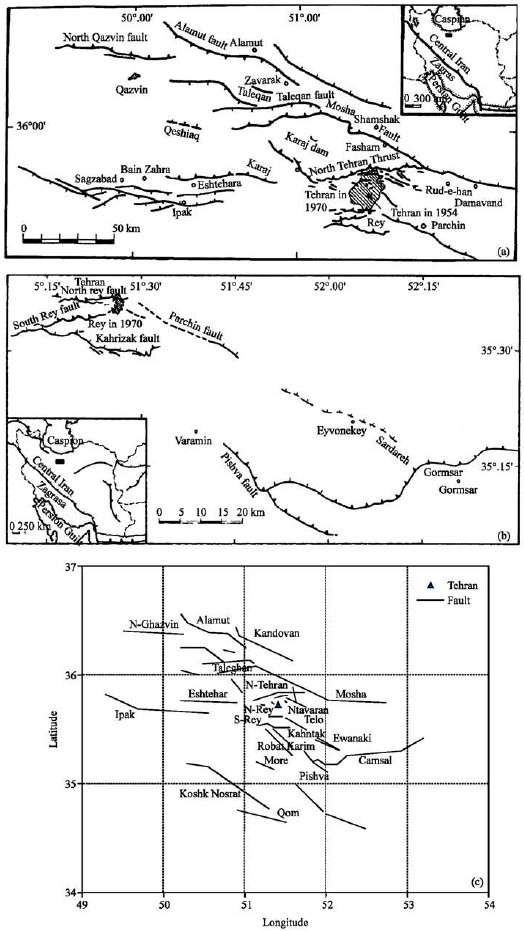
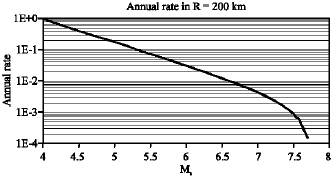
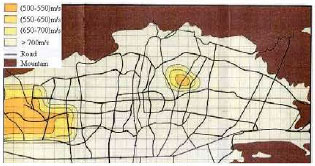
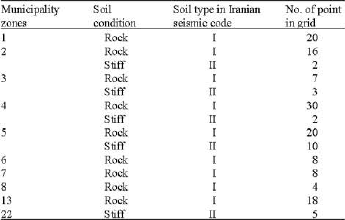
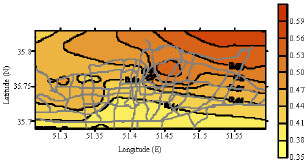
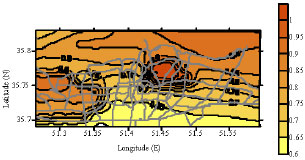
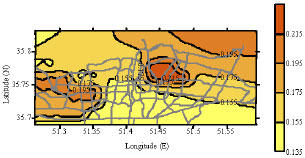
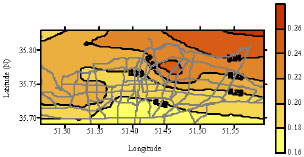
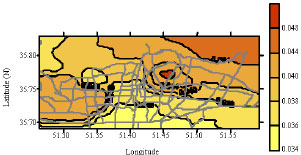
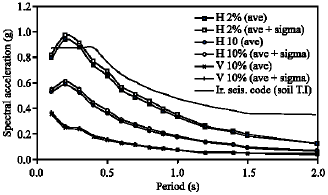
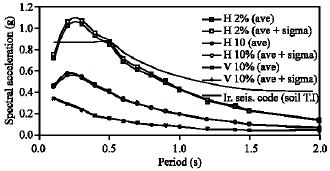
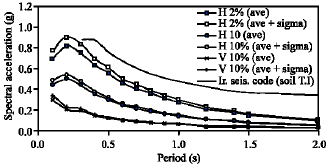
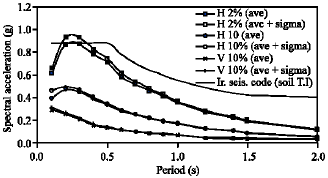
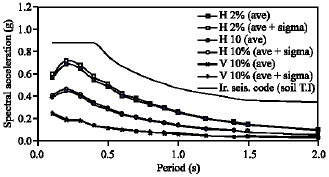
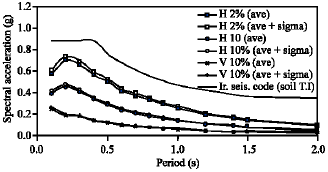
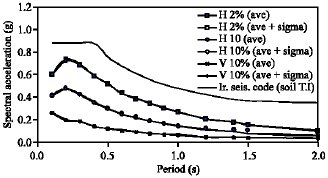
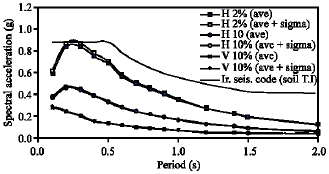
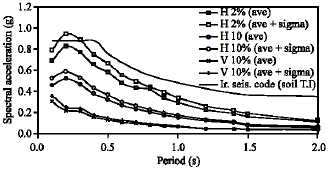
Research Article
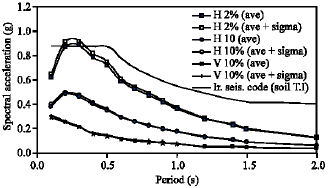
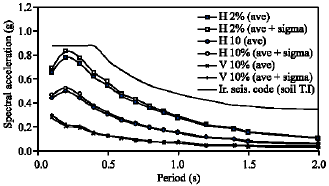
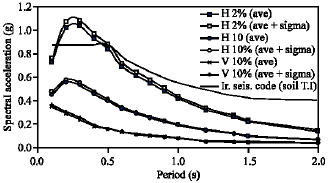
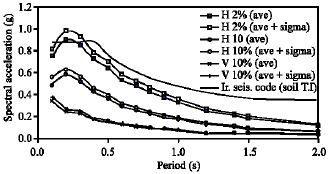
Uniform Hazard Spectra for Different Northern Part of Tehran, Iran
Center of Excellence for Fundamental Studies in Structural Engineering, College of Civil Engineering, Iran University of Science and Technology, Narmak, Tehran 16846, Iran
Seyed Ali Razavian Amrei
Building and Housing Research Center, Iran University of Science and Technology, Tehran, Iran
Ramin Motamed
Department of Civil Engineering, University of Tokyo, Japan
Behnoud Ganjavi
Department of Civil Engineering, Faculty of Engineering, Mazandaran University, Babol, Iran