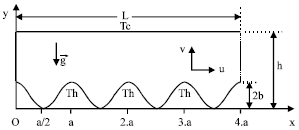
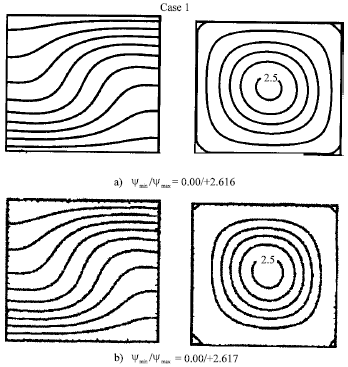
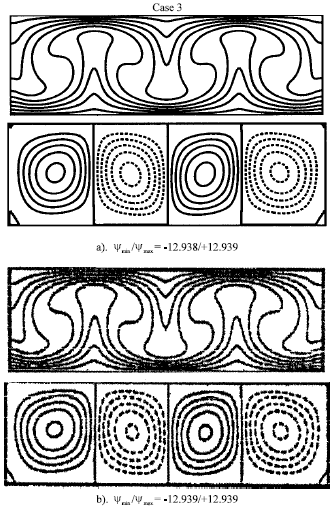
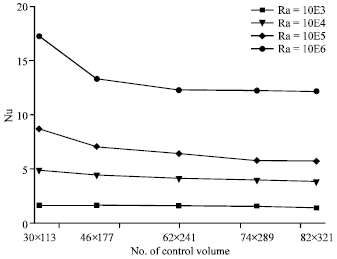
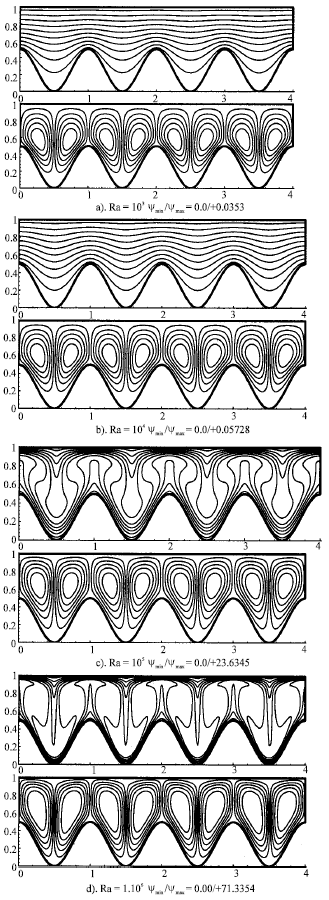
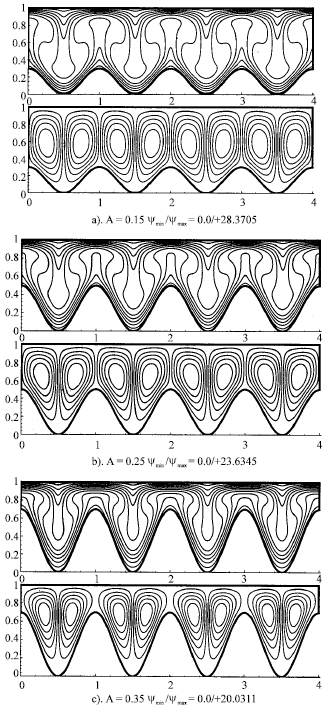
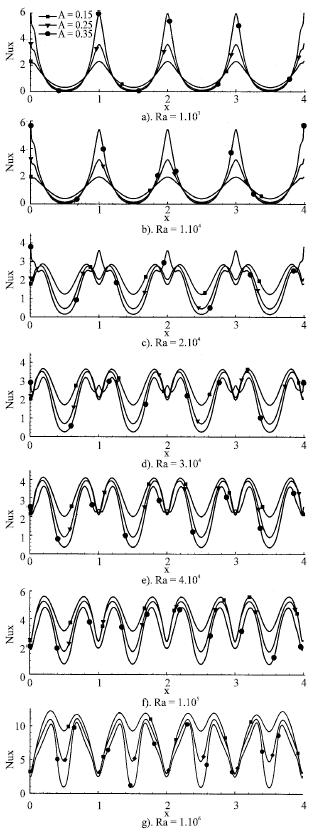
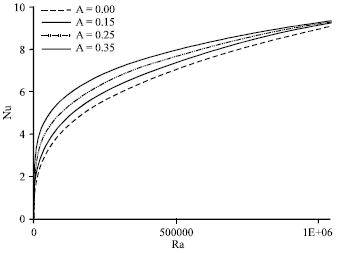
Research Article
Natural Convection in a Horizontal Wavy Enclosure
Institut de Genie Mecanique, C.U. Bechar, Bechar, Algerie
Rebhi Mebrouk
Institut de Genie Mecanique, C.U. Bechar, Bechar, Algerie
Belkacem Abdellah
Institut de Genie Mecanique, C.U. Bechar, Bechar, Algerie
Bouhadef Khadidja
L.T.P.M.P. Faculte de Genie Mecanique et de Genie des Proc�des U.S. T.H.B., Algerie