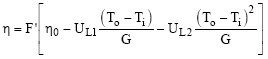Research Article
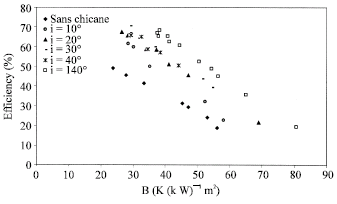
Influence of Obstacles with Wing Delta Shape on Flat-Plate Air Solar Collector Efficiency
Laboratoire D��nergies Nouvelles et Renouvelables,de l�Institut National Polytechnique Felix Houphou�t Boigny, Yamoussoukro, C�te d�Ivoire
K. Konan
Departement Genie Electrique et electronique de l�Institut,National Polytechnique Houphou�t Boigny-BP 1093 Yamoussoukro, C�te d�Ivoire
J.K. Saraka
Laboratoire D��nergies Nouvelles et Renouvelables,de l�Institut National Polytechnique Felix Houphou�t Boigny, Yamoussoukro, C�te d�Ivoire
T.R. Ori
Laboratoire D��nergies Nouvelles et Renouvelables,de l�Institut National Polytechnique Felix Houphou�t Boigny, Yamoussoukro, C�te d�Ivoire
H.Y. Andoh
Laboratoire D��nergies Nouvelles et Renouvelables,de l�Institut National Polytechnique Felix Houphou�t Boigny, Yamoussoukro, C�te d�Ivoire