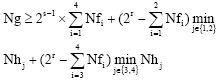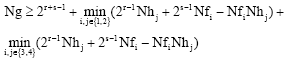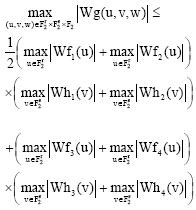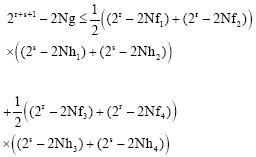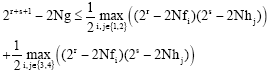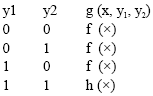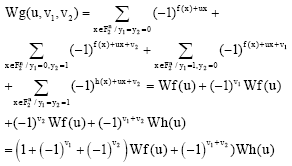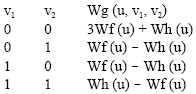Research Article
Secondary Construction of Resilient Functions and Plateaued Functions: Study Their Algebraic Immunity
Department of Electronics, Faculty of Science and Engineenng, Badji Mokhtar University-Skikda LP 26 El-Hadeik Avenue
Doghman Nouredine
Department of Electronics, Faculty of Science and Engineenng, Badji Mokhtar University-Annaba LP 12