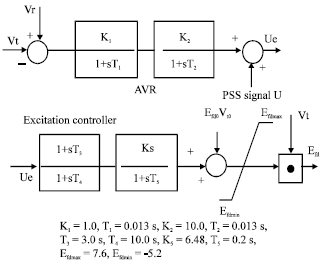
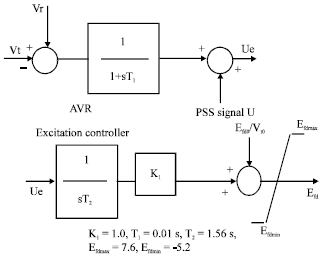
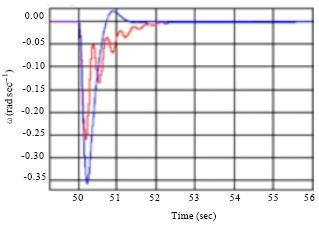
Research Article
Real Time Dynamic Simulation of Retrofitted Turbogenerator in Matlab/Simulink Environment
Laboratory of Electro Mechanic Systems, Algeria
O. Ghorab
Laboratory of Electro Mechanic Systems, Algeria
N.E. Debbache
Laboratory of Electronic, University of Annaba, Algerie