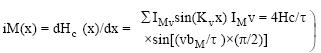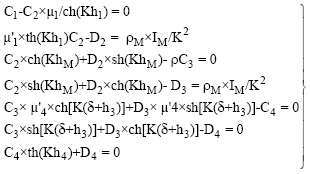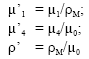Research Article
Use of Permanent Magnets for the Linear Asynchronous Motors Braking in Transport
Laboratoire des syst�mes electromecanique Universite Annaba, Algerie
N. Ghorab
Laboratoire des syst�mes electromecanique Universite Annaba, Algerie
Elena Sokolova
Laboratoire d3 electronique Universite Annaba, Algerie
N.E. Debbache
Laboratoire d3 electronique Universite Annaba, Algerie