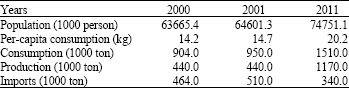
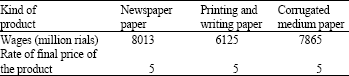
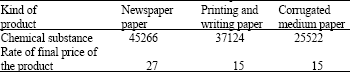
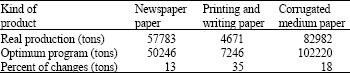
Research Article
Determining an Optimum Model for Production in Paper Industry: Case Study of Iranian Mazandaran Wood and Paper Industries
Faculty of Natural Resources, University of Tehran, Iran
Mohammad Aghapour
Faculty of Agriculture, University of Tehran, Iran