Research Article
Characterization of Areas of Pixels Modified During the Generation of Multiscale Digital Elevation Models
Science and Technology Research Institute for Defense (STRIDE), Ministry of Defence, Malaysia
Feature detection and characterization often need to be performed at different of scales measurement. Wood (1996a, b) shows that analysis of a location at multiple scales allows for a greater amount of information to be extracted from a DEM about the spatial characteristics of a feature. The term scale refers to combination of both spatial extent and spatial detail or resolution (Tate and Wood, 2001). A number of research efforts have been conducted to characterize geomorphological features, such as drainage and ridge networks (Radhakrishnan, 2002, 2003, 2004; Sagar et al., 2003; Tay et al., 2005), catchments (Dinesh, 2007a) and mountains (Dinesh, 2007b, c, d; Dinesh and Fadzil, 2007a, b), using the variation in the spatial extent over which these features are defined.
This study is aimed at characterizing the areas of pixels modified during the generation of multiscale Digital Elevation Models (DEMs). The proposed procedure is employed to compute a scale-independent surface roughness parameter of the terrain of DEMs.
The global digital elevation model (GTOPO30) of great basin: The DEM in Fig. 1 shows the area of Great Basin, Nevada, USA. The area is bounded by latitude 38° 15’ to 42° N and longitude 118° 30’ to 115° 30’W. The DEM was rectified and resampled to 925 m in both x and y directions. The DEM is a Global Digital Elevation Model (GTOPO30) and was downloaded from the USGS GTOPO30 website (http://edcwww.cr.usgs.gov/landdaac/ gtopo30/gtopo30.html). GTOPO30 DEMs are available at a global scale, providing a digital representation of the Earth’s surface at a 30 arc-sec sampling interval. The land data used to derive GTOPO30 DEMs are obtained from digital terrain elevation data (DTED), the 1-degree DEM for USA and the Digital Chart of the World (DCW). The accuracy of GTOPO30 DEMs varies by location according to the source data.
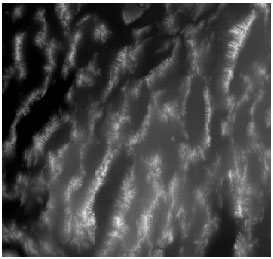 | |
| Fig. 1: | The GTOPO30 DEM of Great Basin. The elevation values of the terrain (minimum 1005 m and maximum 3651 m) are rescaled to the interval of 0 to 255 (the brightest pixel has the highest elevation). The scale is approximately 1:3,900,00 |
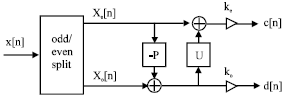 | |
| Fig. 2: | Lifting stage: split, predict, update; ke and ko normalize the energy of the underlying scaling and wavelet functions. (Source: Claypoole and Baraniuk, 2000) |
The DTED and the 1-degree dataset have a vertical accuracy of ±30 m while the absolute accuracy of the DCW vector dataset is ±2000 m horizontal error and ±650 vertical error (Miliaresis and Argialas, 2002).
Generation of multiscale DEMs using the lifting scheme: In this study, multiscaling is performed using the lifting scheme (Sweldens, 1996, 1997). The lifting scheme is a flexible technique that has been used in several different settings, for easy construction and implementation of traditional wavelets and of second generation wavelets, such as spherical wavelets. Lifting consists of the following three basic operations (Fig. 2):
Step 1: Split
The original data set x[n] is divided into two disjoint subsets, even indexed points xe[n] = x[2n] and odd indexed points x0[n] = x[2n+1].
Step 2: Predict
The wavelet coefficients d[n] are generated as the error in predicting x0[n] from xe[n] using the prediction operator P:
| (1) |
Step 3: Update
Scaling coefficients c[n] that represent a coarse approximation to the signal x[n] are obtained by combining xe[n] and d[n]. This is accomplished by applying an update operator U to the wavelet coefficients and adding to xe[n]:
| (2) |
These three steps form a lifting stage. Using a DEM as the input, an iteration of the lifting stage on the output c[n] creates the complete set of multiscale DEMs cj[n] and the elevation loss caused by the change of scale dj[n].
Multiscale DEMs of the Great Basin region are generated by implementing the lifting scheme on the DEM of Great Basin using scales of 1 to 20. As shown in Fig. 3, as the scale increases, the merge of small regions into the surrounding grey level regions increases, causing removal of fine detail in the DEM. The fine detail in DEMs represents crenulations, which are used to extract hydrological features from DEMs. Convex crenulations are used to extract ridge networks while concave crenulations are used to extract drainage networks (Gilbert, 1909; Howard, 1994; Rodríguez-Iturbe and Rinaldo, 1997). The distribution of convex and concave regions over a terrain indicates the surface roughness of the terrain. The removal of convex and concave regions from the terrain during the multiscaling process results in the terrain becoming smoother.
Characterization of pixels modified during the generation of multiscale DEMs: For each scale r, the area of pixels modified S(r) (Fig. 4) is computed. The normalized probability functions s(r) are computed as the ratio of the areas of pixels modified to the area of the original DEM S0. A plot of the normalized probability functions against the scales (Fig. 5).
| (3) |
The computed values of s(r) are used to compute two important grayscale granulometric complexity measures:
Average size AS: This indicates the average size of convex and concave regions on the terrain of the DEM.
Average roughness H: This indicates surface roughness of the terrain of the DEM due to the convex and concave region distribution averaged over the area of the terrain.
AS and H are computed using the following equations, which are due to Maragos (1989):
| (4) |
| (5) |
AS and H are computed to be 42.03 and 2.34, respectively. In the past few decades, the quantitative computation of surface roughness has received increasing attention due to its importance in numerical surface study. Hoffman and Krotkov (1989) report that surface roughness measurements must have the following properties:
 | |
| Fig. 3: | Multiscale DEMs genrated using scales of (a) 1, (b) 3, (c) 5, (d) 10, (e) 15, (f) 20 |
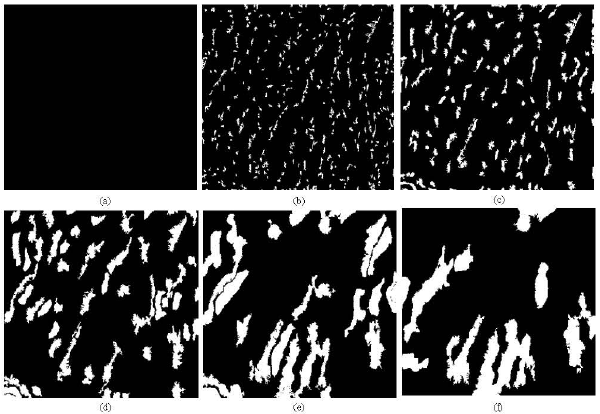 | |
| Fig. 4: | Mask of pixels modified during the multiscaling process for the corresponding multiscale DEMs in Fig.3 |
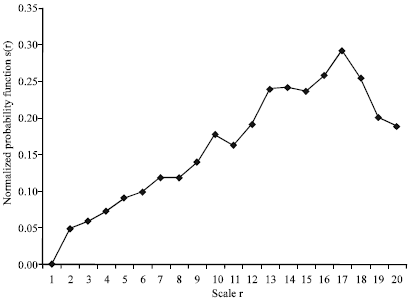 | |
| Fig. 5: | Plot of the normalized probability function s(r) against the scale r |
| • | Must discriminate between surfaces of different amplitudes, frequencies and correlation |
| • | Be an intrinsic property of the surface, invariant with respect to rotation or translation |
| • | Be a local, not a global measure of the surface |
| • | Have intuitive or physical meaning. |
A number of algorithms have been employed to compute surface roughness; a summary can be found in Shepard et al. (2001). The most commonly used roughness parameter and the easiest to obtain, is the Root-Mean-Square (RMS) height, or the standard deviation of heights above the mean (Brock, 1983). The profile is first detrended by subtracting a best fit linear function from the data, leaving a series of heights with a mean value of zero. This approach is insensitive to amplitude differences and is not a good frequency discriminator. An alternative approach is to fit a plane to a surface and use the error as an estimate of the surface roughness (Wilcox and Gennery, 1987). In the case of two sinusoidal surfaces of differing frequencies, plane fitting suffers from a fundamental shortcoming by producing the same roughness estimation. Stone and Dugundji (1965) propose a method of computing surface roughness using Fourier analysis. This method measures roughness along specific directions of a surface and includes amplitude, frequency and autocorrelation terms. This approach provides surface roughness parameters that have consistent representation in the frequency domain. However, as it depends on the direction of measurement, it is influenced by the rotation and translation of the surface. The slope and intercept of the logarithmic plot of the power spectrum of the terrain profile is reported as a roughness parameter by van Zyl et al. (1991). However, there is no simple correspondence between the intercept or the slope of the logarithmic plot of the power spectrum and commonly used roughness measures. Other reported roughness measures, developed to overcome these shortfalls, include effective slope (Miller and Parsons, 1990; Campbell and Garvin, 1993), autocorrelation length (Turcotte, 1997) and median and absolute slope (Kreslavsky and Head, 1999). These algorithms, which operate at singular scales of measurement, provide scale-dependant roughness parameters.
The proposed procedure takes into account the amplitudes and frequencies of the terrain, ensuring a realistic measure of the roughness of the terrain. As the proposed procedure does not depend on direction of measurement, it is invariant with respect to rotation and translation. The parameters AS and H are intuitive; surfaces with large amplitudes have larger values of AS and H as compared to surfaces with smaller amplitudes. The proposed procedure takes into account the removal of convex and concave regions across multiple scales and is as able to provide a scale-independent roughness parameter.
In this study, the characterization of the areas of pixels modified during the generation of multiscale DEMs was performed. The computed areas were divided with the area of the DEM to obtain the normalized probability functions, which were used to compute to the average size of convex and concave regions on the terrain of the DEM and the scale-independent average roughness of the terrain of the DEM due to the convex and concave region distribution averaged over the area of the terrain. The proposed procedure provides a surface roughness parameter that is realistic with respect to the amplitudes and frequencies of the terrain, invariant to with respect to rotation and translation and has intuitive meaning.
In general, the larger the average size of the convex and concave regions in the terrain of DEM, the larger is the average roughness of the terrain. Work is being done to further quantify the relationship between the average size of the convex and concave regions and the average roughness of the terrain of the DEM.
The author is grateful to Dr. George Miliaresis, Geology Department, University of Patras, Greece, for his comments that have helped strengthen this study.