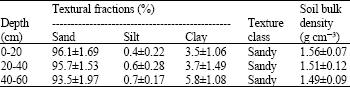
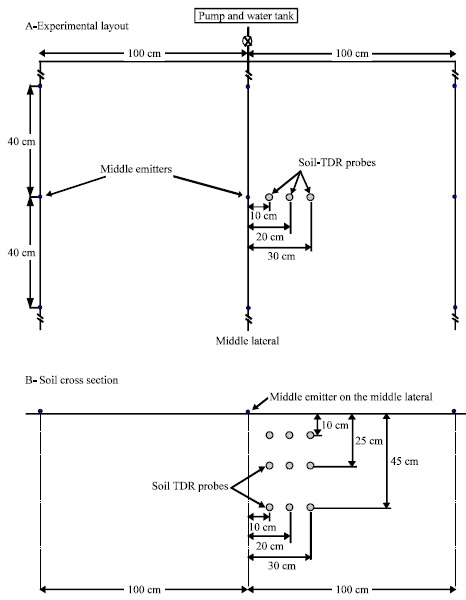
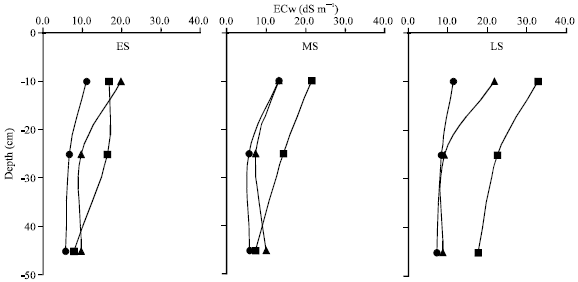
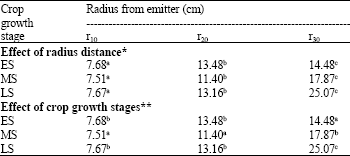
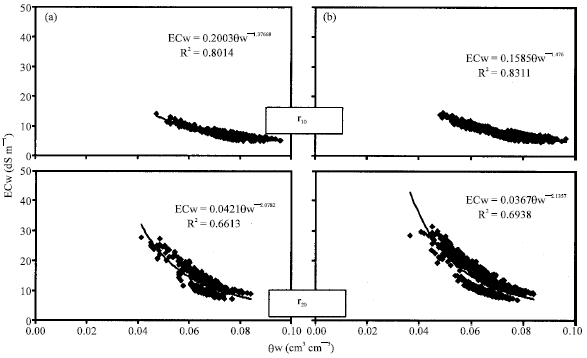
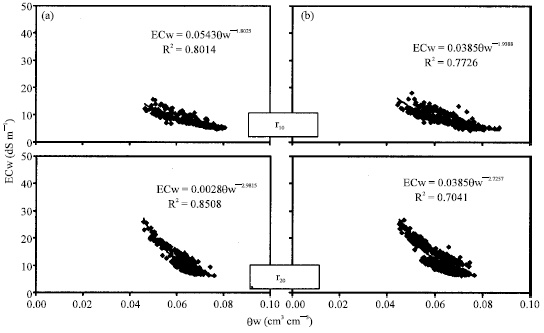
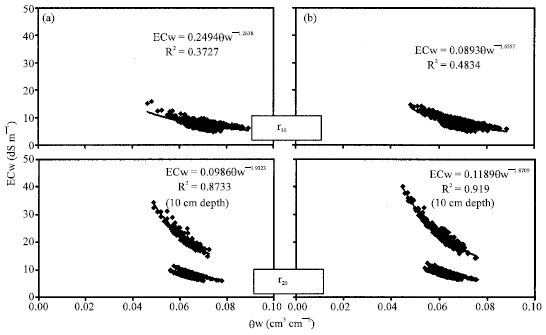
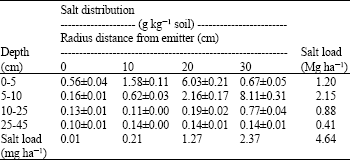
Research Article
Water Flow and Solute Transport Under Drip Irrigation in Sand Dune Field
Agricultural Engineering Research Institute, P.O. Box 31585-845, Karaj, Iran
T. Yamamoto
Arid land Research Center, Tottori University, 1390 Hamasaka, Tottori 680-0001, Japan
M. Inoue
Arid land Research Center, Tottori University, 1390 Hamasaka, Tottori 680-0001, Japan
M. Akbari
Agricultural Engineering Research Institute, P.O. Box 31585-845, Karaj, Iran