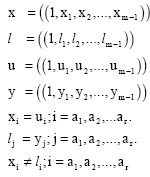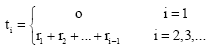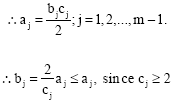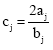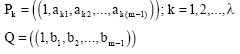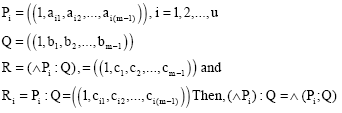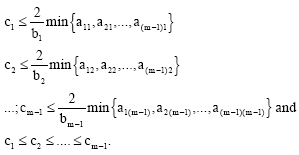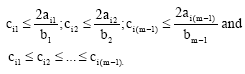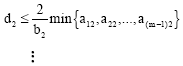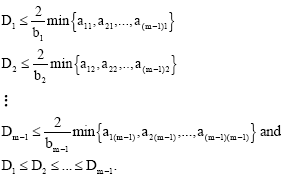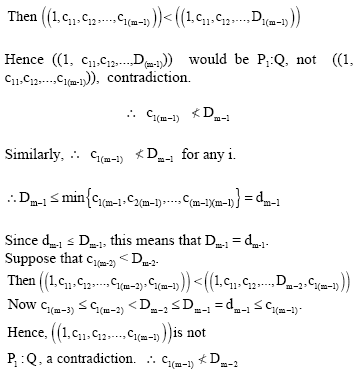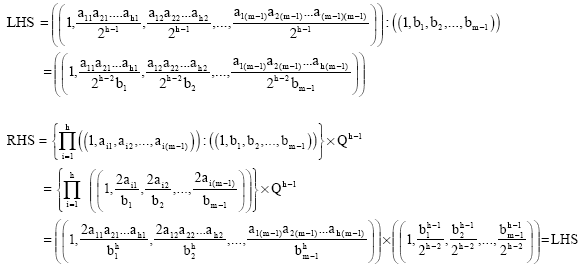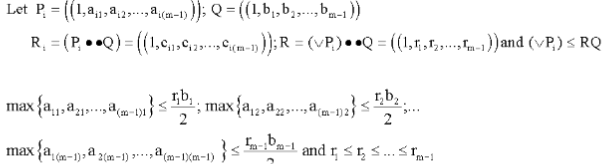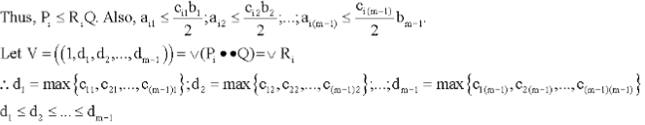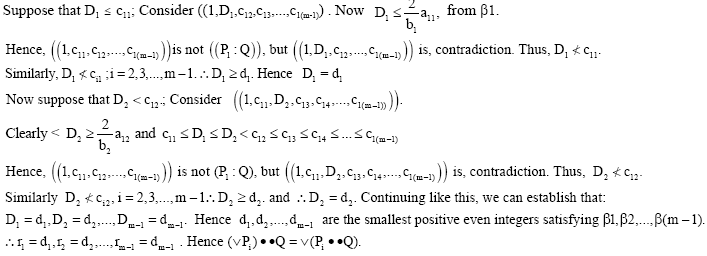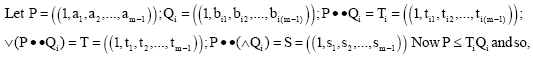Research Article
Algebraic Structure of Lattices of SK Partitions
Department of Mathematics and Computer Science, Faculty of Science and Agriculture, St. Augustine Campus, The University of the West Indies, St. Augustine, Trinidad, West Indies
Norris Sookoo
Department of Mathematics and Computer Science, Faculty of Science and Agriculture, St. Augustine Campus, The University of the West Indies, St. Augustine, Trinidad, West Indies
Ashok Sahai
Department of Mathematics and Computer Science, Faculty of Science and Agriculture, St. Augustine Campus, The University of the West Indies, St. Augustine, Trinidad, West Indies