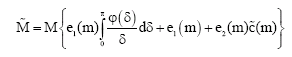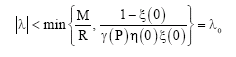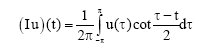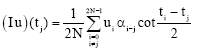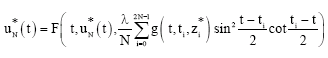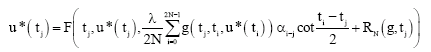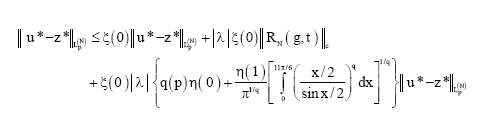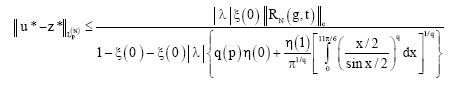Research Article
On the Approximate Solution of Singular Integral Equations with Hilbert Kernel
Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
S.M. Amer
Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt