Research Article
Saturation Intensity in Excited Channel for Nonlinear Medium With Coincident Absorption and Emission Bands-Part I
Department of Applied Physics, Faculty of Science, Tafila Technical University, Jordan
An optical properties of dye solutions were used to study nonlinear processes such as: four-wave mixing, amplification and holography (Shalaev, 2002; Sarychev and Shalaev, 2000; Poliakov et al., 1999). The interaction of light beams with nonlinear media appears in many nonlinear processes such as refraction, interference, thin films, optical bistability, phase-conjugation and others (Poliakov et al., 1998; Podolskiy et al., 2003; Agishev et al., 1998; Popov and Shalaev, 1980a). The three-level model were studied using averaged Einstein coefficients for different media (Bolotskikh et al., 1986; Agishev et al., 1998; Tichonov and Shpak, 1979).
The control of the nonlinear processes is very important to study many optical properties. The three-level model for nonlinear media gives ability to control the nonlinear processes by independent light beam (Popov et al., 2000; Agishev et al., 1998; Popov and Shalaev, 1980b). In this model the dye solution can be excited by light fields in which, first group of light fields acts in principal channel (S0-S1) and other group acts in excited channel (S1-S2). Light fields (with intensity I23 at frequency ω) can involve a nonlinear processes in excited channel and other light field (optical pumping with intensity I12 at frequency ωo) acts in the principal channel (Agishev et al., 1998; Rubanov et al., 2000). In this case,the nonlinear processes can be controlled by independent light beam (optical pumping), acting in the principal channel.
The phase response of nonlinear media depends on the intensities and frequencies of light fields acting in each of principal and excited channels. The saturation intensity in principal channel was studied for nonlinear medium with Gaussian form of mirror-symmetric absorption and emission bands with Stokes shift (Addasi, 2005).
The aim of this theoretical study is to find an optimal conditions of saturation intensity in excited channel for nonlinear media with coincident absorption and emission bands.
THEORY
The extinction coefficient in excited channel at frequency ω can be written as follows:
| (1) |
where:
is the absorption coefficient in principal channel, Ni is the population of i-energy level; N is the number of molecules in the unit volume and v = c/n is the light velocity.
Using the balance equations under a double frequencies excitation of dye solution modeled by three-level configuration we can rewrite Eq. 1 in the form:
| (2) |
| χ0 | = | NħcB12(ω0)/2v, |
| χ0(ω0) | = | Linear extinction coefficient, |
| Pij | = | Total probability of spontaneous and radiationless transitions in the i-j channel, |
| K | = | 1+JI12 + aI23 + bI12I23, |
| a | = | B32/vp32, |
| J | = | (B12 + B21)/vp21, |
| b | = | B12B23 + aJ. |
The Einstein coefficients B12(ω0), B21(ω0) are determined at the frequency of radiations (ω0) in the principal channel S0-S1. At the same time B23(ω); B32(ω) are determined at frequency of radiations (ω) in the excited channel S1-S2.
The saturation intensity in excited channel (I23sat) is defined as the value of radiation intensity, for which the absorption in this channel is decreasing to half of its maximum value:
| (3) |
| (4) |
where, ![]() is the extinction coefficient for excited channel in absence of radiations in this channel. Simply we can consider the nonlinear processes in excited channel as a processes in two-level model (S1-S2) with varies population of first energy level and with linear extinction coefficient
is the extinction coefficient for excited channel in absence of radiations in this channel. Simply we can consider the nonlinear processes in excited channel as a processes in two-level model (S1-S2) with varies population of first energy level and with linear extinction coefficient ![]() , depending on optical pumping with intensity I12 at frequency ωo as an external factor.
, depending on optical pumping with intensity I12 at frequency ωo as an external factor.
The saturation intensity in the excited channel has the value:
| (5) |
ANALYSIS AND RESULTS
Equation (5) shows that, the saturation intensity in excited channel ![]() has a monotonic dependence on radiation intensity in principal channel (I12) and for effective excitation in principal channel, the saturation intensity has enough small value. The saturation intensity in excited channel (
has a monotonic dependence on radiation intensity in principal channel (I12) and for effective excitation in principal channel, the saturation intensity has enough small value. The saturation intensity in excited channel (![]() ) has an optimum values as a function of frequency.
) has an optimum values as a function of frequency.
Using Eq. 5 we can obtain numerical analysis for dependence of saturation intensity ![]() on intensity in principal channel (I12) and on frequency tuning of radiations in both principal and excited channels (η12, η23).
on intensity in principal channel (I12) and on frequency tuning of radiations in both principal and excited channels (η12, η23).
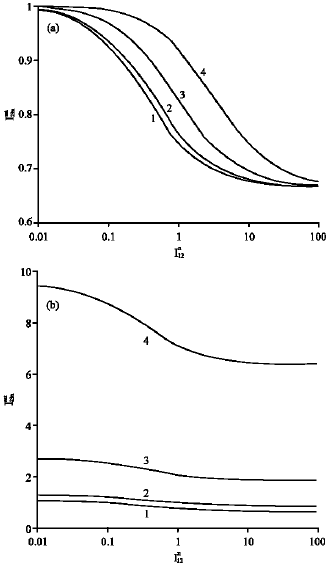 | |
| Fig. 1: | Dependence of saturation intensity in excited channel |
For this dependence, nonlinear medium with a Gaussian form of coincident mirror-symmetric absorption and emission bands (ωij = ωji, ηij = ηji) is taken into consideration. Where, the frequency tuning of radiations in principal (η12 = (ω0-ω12)/Δ12) and excited (η23 = (ω-ω23)/Δ22) channels are used to find Einstein coefficients Bij and Δij, ωij. Where, Δij, ωij are the profile halfwidth and the centre of i-j channel.
Equation 5 and Fig. 1a and b show the monotonic dependence of saturation intensity in excited channel on radiation intensity in the principal channel I12. Figure 1a shows the dependence for different frequency tuning of radiations in principal channel η12 = 0 (curve 1),"0.5 (curve 2), ±1.0 (curve 3) and ±1.5 (curve 4) at radiations in excited channel tuned in the centre of absorption band η23 = 0.
 | |
| Fig. 2: | Dependence of saturation intensity in excited channel |
The dependence of saturation intensity in excited channel ![]() on radiation intensity in the principal channel I12 is shown in Fig. 1b, at frequency tuning in principal channel η12 = 0, for different values of frequency tuning in excited channel η23 = 0 (curve 1); ±0.5 (curve 2), ±1.0 (curve 3) and ±1.5 (curve 4).
on radiation intensity in the principal channel I12 is shown in Fig. 1b, at frequency tuning in principal channel η12 = 0, for different values of frequency tuning in excited channel η23 = 0 (curve 1); ±0.5 (curve 2), ±1.0 (curve 3) and ±1.5 (curve 4).
Figure 1 shows that, for enough large intensity of radiations in principal channel (I12B12max/vp21>1), the saturation intensity in excited channel reaches a small values ![]()
From Eq. 5 the saturation intensity in excited channel![]() for coincident absorption and emission bands, has optimum values (minimum) at radiations frequency tuned into the centre of principal absorption and emission bands η12 = η21 = 0, (Fig. 2). In addition, the optimum of
for coincident absorption and emission bands, has optimum values (minimum) at radiations frequency tuned into the centre of principal absorption and emission bands η12 = η21 = 0, (Fig. 2). In addition, the optimum of ![]() is occurred at frequency of radiations, in excited channel, tuned into the centre of excited absorption and emission bands (η23 = η32 = 0,) (Fig. 3).
is occurred at frequency of radiations, in excited channel, tuned into the centre of excited absorption and emission bands (η23 = η32 = 0,) (Fig. 3).
Figure 2 and 3 show that, the saturation intensity in excited channel ![]() depends strongly on the intensity of radiations in principal channel (I12) for different frequency tuning in principal channel (η12) and weekly depends on the intensity of radiations in principal channel (I12) for different frequency tuning in excited channel (η23).
depends strongly on the intensity of radiations in principal channel (I12) for different frequency tuning in principal channel (η12) and weekly depends on the intensity of radiations in principal channel (I12) for different frequency tuning in excited channel (η23).
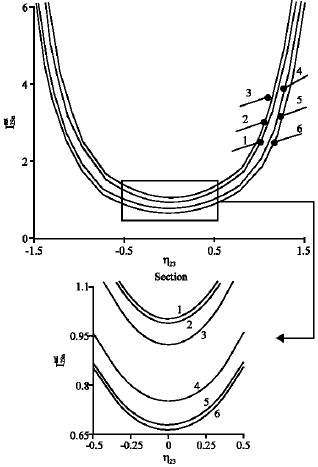 | |
| Fig. 3: | Dependence of saturation intensity in excited channel |
The saturation processes in excited channel are achieved with small enough intensity![]() when an effective excitation of molecules occurs in principal channel (I12B12max/vp21>1;-1<η12<1)). The radiations in excited channel must have a frequency tuned near the centre of excited absorption and emission bands (-0.5<η23(32) <0.5), to achieve the saturation processes. The control of nonlinear effects in excited channel can simply reach by external independent radiation in principal channel.
when an effective excitation of molecules occurs in principal channel (I12B12max/vp21>1;-1<η12<1)). The radiations in excited channel must have a frequency tuned near the centre of excited absorption and emission bands (-0.5<η23(32) <0.5), to achieve the saturation processes. The control of nonlinear effects in excited channel can simply reach by external independent radiation in principal channel.