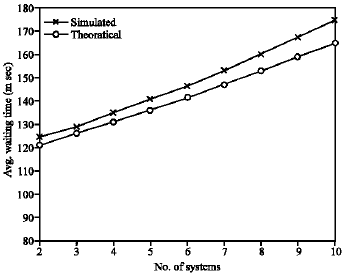
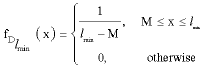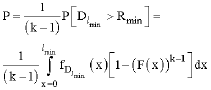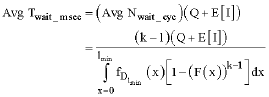Research Article
On Average Waiting Time in Shared Dynamic Spectrum Allocation
Institute of Mobile Communications, Southwest Jiaotong University, Chengdu, 610031, China
Pingzhi Fan
Institute of Mobile Communications, Southwest Jiaotong University, Chengdu, 610031, China
Yi Pan
Department of Computer Science, Georgia State University, Atlanta, GA30303-4110, USA