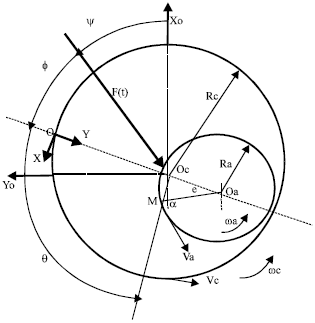
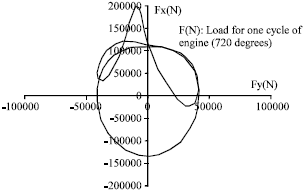
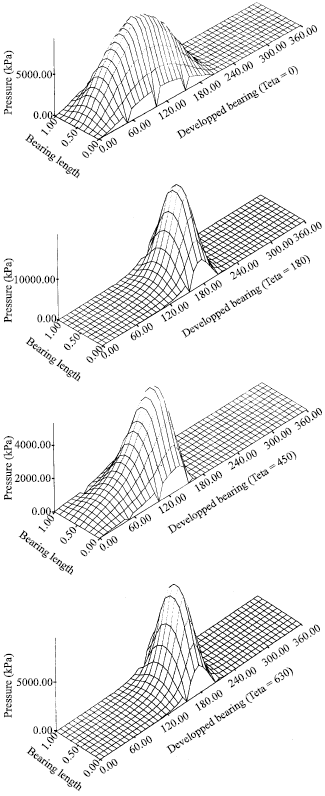
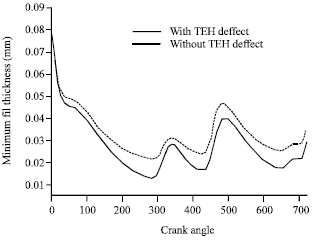
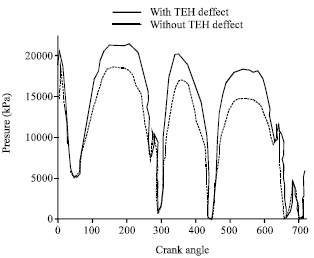
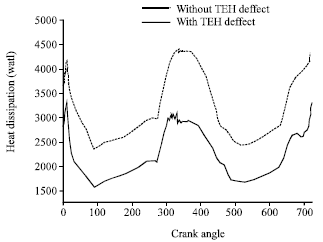
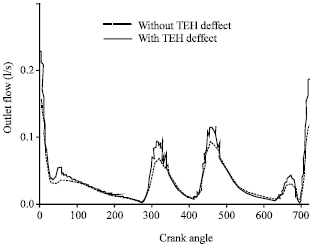
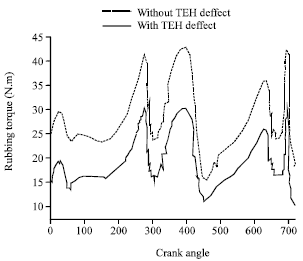
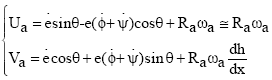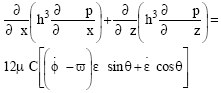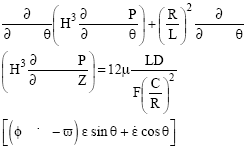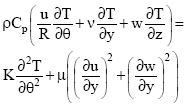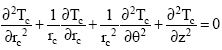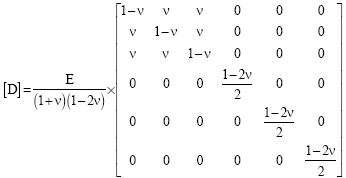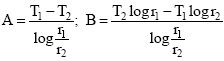Research Article
Effects of the Elastic Strain and Dilation in the Big End Journals
Department of Mechanical Engineering, U.S. T. Oran-Algeria
Abdelhamid Bounif
Laboratory of the Gas Fuels and Environment U.S. T. Oran-Algeria
Patrick Maspeyrot
Laboratory of solids Mechanics, SP2MI, Poitiers France
Towfik Tamine
Department of Mechanical Engineering, U.S. T. Oran-Algeria