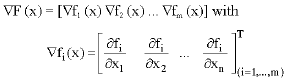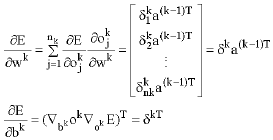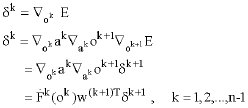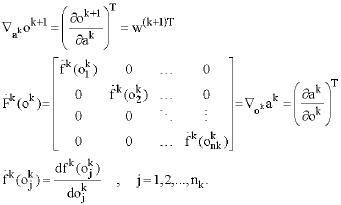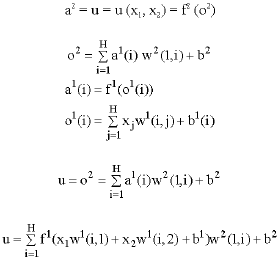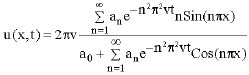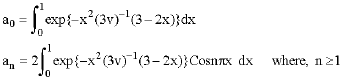Research Article
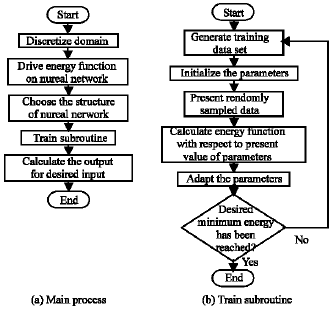
Feedforward Neural Network for Solving Partial Differential Equations
Department of Electrical Engineering, Razi University, Kermanshah-67149, Iran
Behnam Karami
Department of Electrical Engineering, Razi University, Kermanshah-67149, Iran