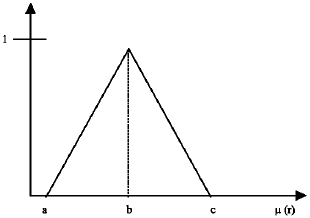
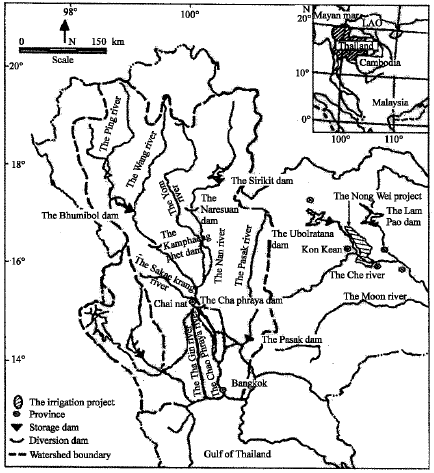
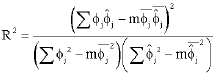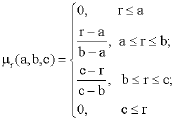Research Article
An Estimation of Irrigation Efficiency of Limited Water Resource Area
Faculty of Engineering, Mahasarakham University, Mahasarakham, 44150, Thailand
Chavalit Chaleeraktrakoon
Department of Civil Engineering, Faculty of Engineering, Thammasat University,Klong Luang, Pathumthani, 12120, Thailand