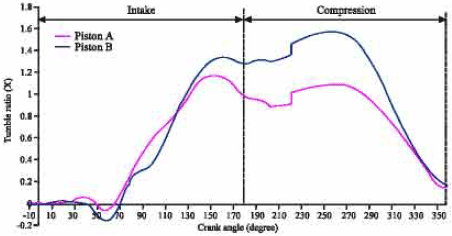
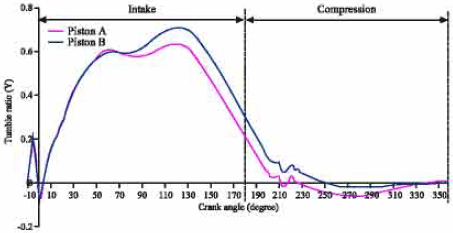
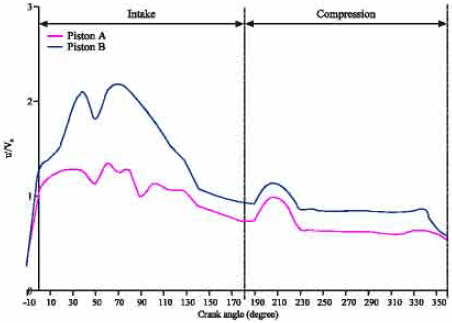
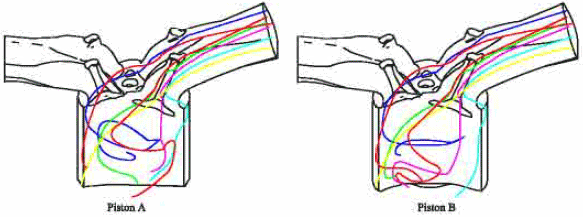
Research Article
A Computational Fluid Dynamics Study of Cold-flow Analysis for Mixture Preparation In a Motored Four-stroke Direct Injection Engine
Department of Mechanical and Materials Engineering, National University of Malaysia,UKM Bangi 43600, Malaysia
Shahrir Abdullah
Department of Mechanical and Materials Engineering, National University of Malaysia,UKM Bangi 43600, Malaysia
Azhari Shamsudeen
Department of Mechanical and Materials Engineering, National University of Malaysia,UKM Bangi 43600, Malaysia