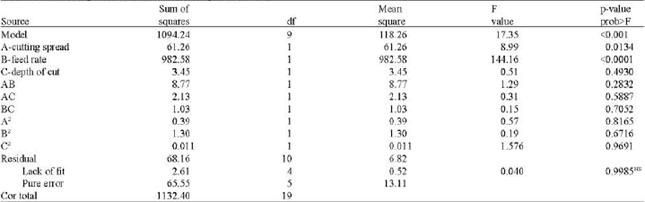
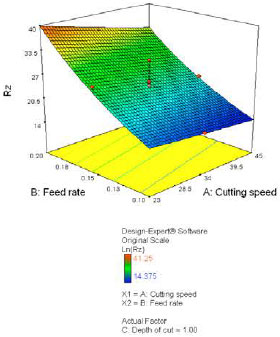
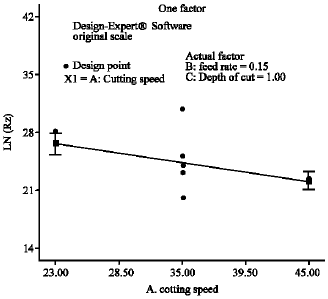
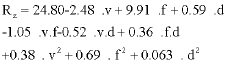Research Article
Empirical Modeling of Surface Roughness in turning process of 1060 steel using Factorial Design Methodology
Department of Mechanical Engineering, University of Urmia, Ermia, Iran
M. Eskandarzade
Department of Mechanical Engineering, University of Urmia, Ermia, Iran
M. Tahmasebian
Department of Mechanical Engineering, University of Urmia, Ermia, Iran