Research Article
Solving Singular Initial Value Problems in the Second-order Ordinary Differential Equations
Department of Mathematics, Harbin Institute of technology, China
Liu Ming Zhu
Department of Mathematics, Harbin Institute of technology, China









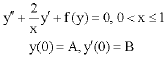
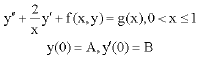
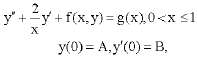
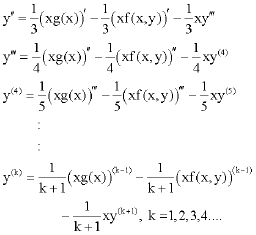
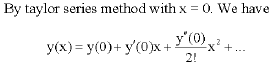

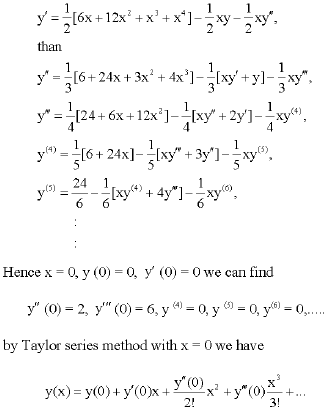
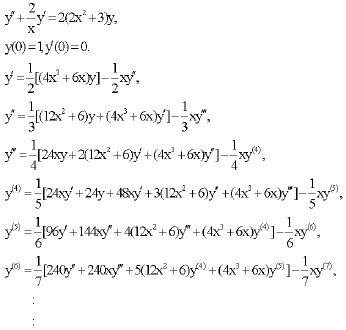
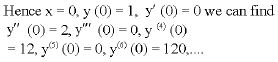

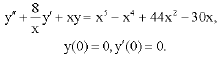

eli aaron ruiz ramos Reply
you can send me an example of the application of Singular Initial Value Problems in the Second-order Ordinary Differential Equations in civil engineering