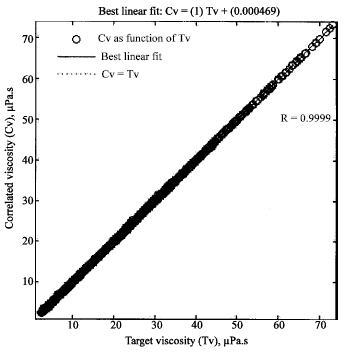
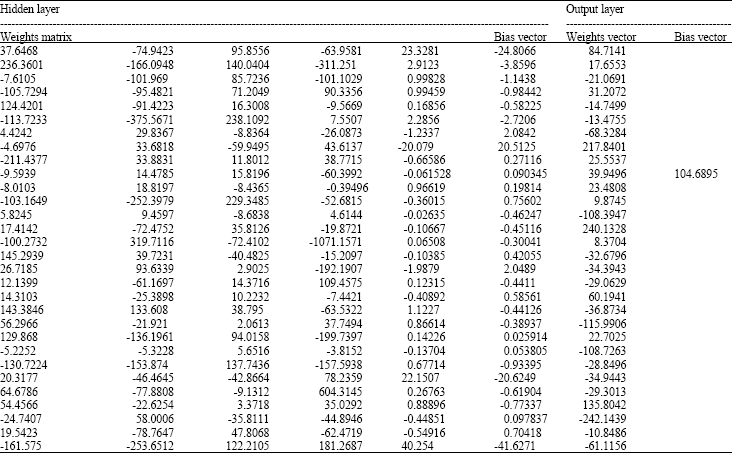
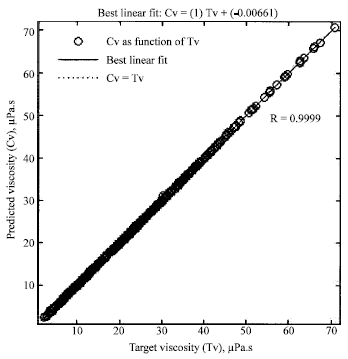
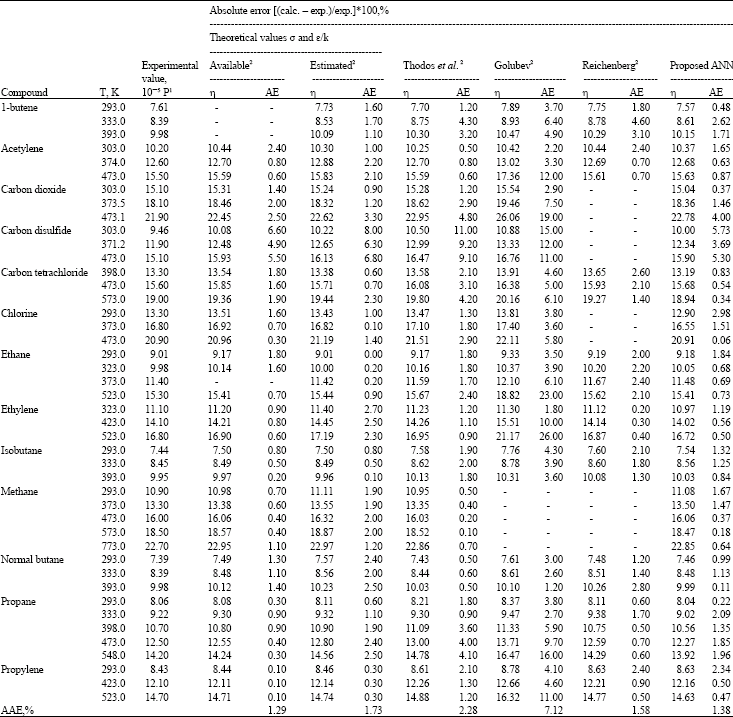
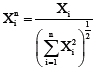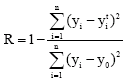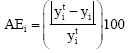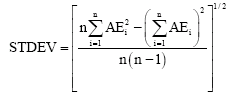Research Article
Viscosity Calculation at Moderate Pressure for Nonpolar Gases via Neural Network
Birine Nuclear Research Center B.P. 180, A�n Oussera W. Djelfa, C.P. 1 7200, Algeria
S. Hanini
LBMPT University of Medea, C.P. 26000, Algeria
F. Souahi
ENP, El HarTach, Algiers, Algeria
B. Mohammedi
Birine Nuclear Research Center B.P. 180, A�n Oussera W. Djelfa, C.P. 1 7200, Algeria
M. Touiza
Birine Nuclear Research Center B.P. 180, A�n Oussera W. Djelfa, C.P. 1 7200, Algeria