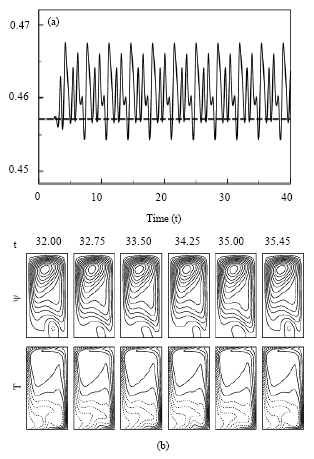
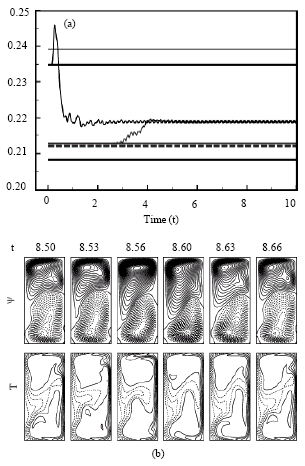
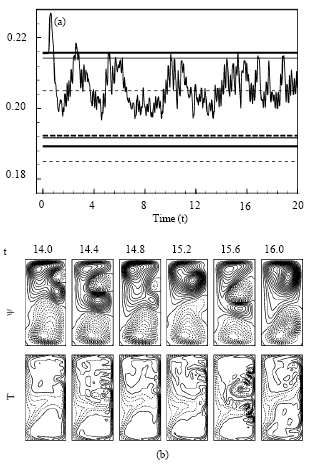
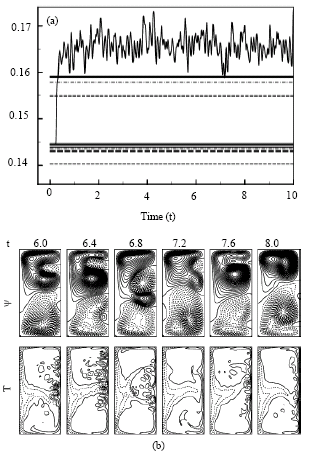
Research Article
Unsteady Solutions of the Thermal Flows Through a Curved Rectangular Duct with Differentially Heated Vertical Sidewalls
Mathematics Discipline, Science, Engineering and Technology School, Khulna University, Khulna-9208, Bangladesh
M.A. Huda
Mathematics Discipline, Science, Engineering and Technology School, Khulna University, Khulna-9208, Bangladesh
S.F. Ahmmed
Mathematics Discipline, Science, Engineering and Technology School, Khulna University, Khulna-9208, Bangladesh
S.M.A. Rahman
Mathematics Discipline, Science, Engineering and Technology School, Khulna University, Khulna-9208, Bangladesh
Munnujahan ara
Mathematics Discipline, Science, Engineering and Technology School, Khulna University, Khulna-9208, Bangladesh