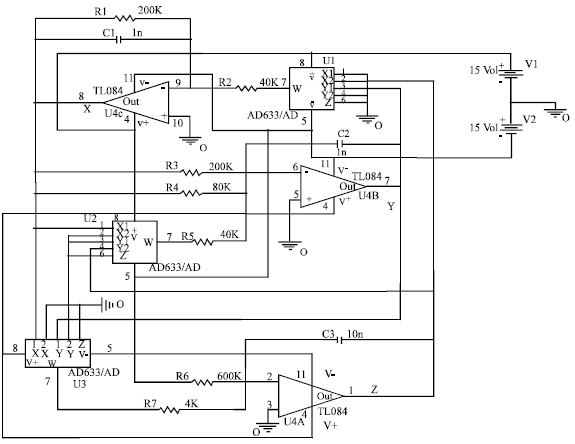
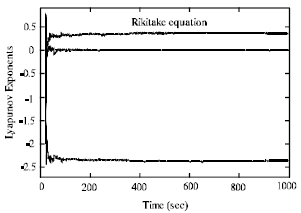
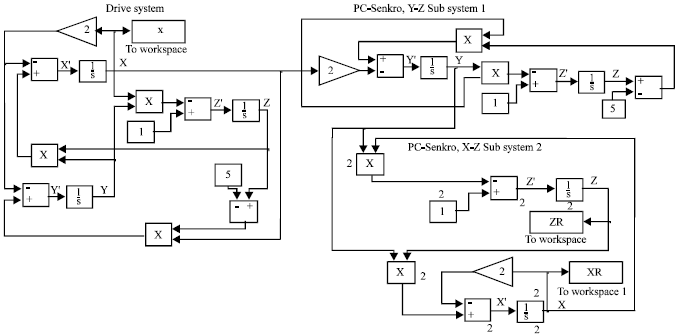
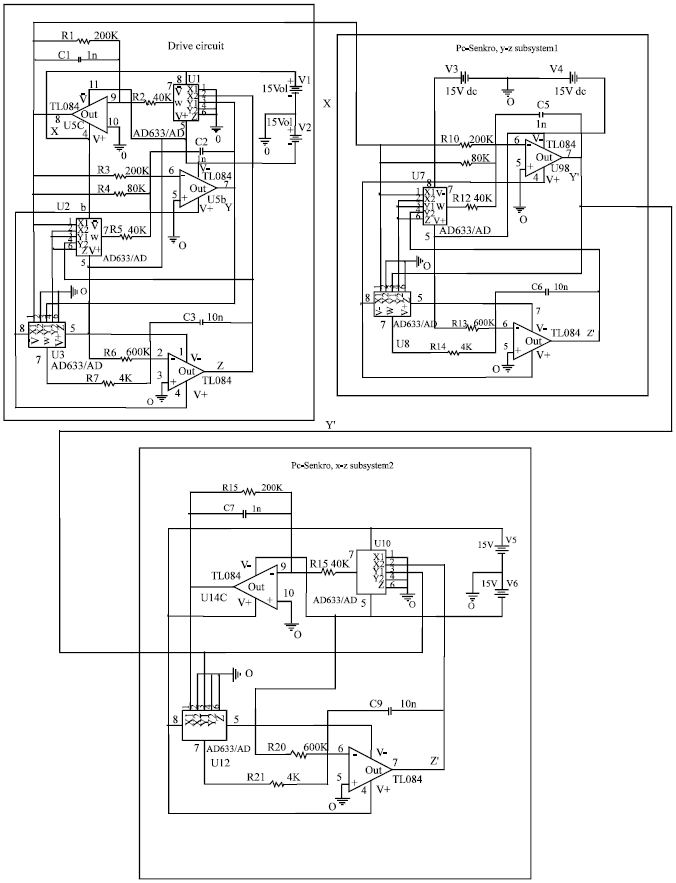
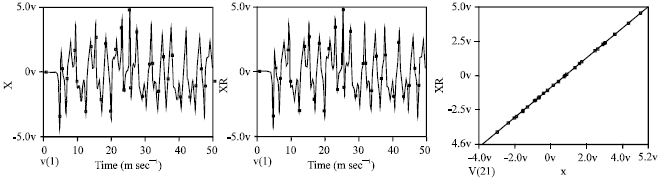
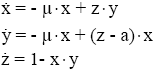Research Article
Rikitake Attractor and It’s Synchronization Application for Secure Communication Systems
Department of Electrical and Electronics Engineermg, Faculty of Engineermg, Sakarya University, Esentepe, Sakarya, Turkey 54040
Yulmaz Uyaroglu
Department of Electrical and Electronics Engineermg, Faculty of Engineermg, Sakarya University, Esentepe, Sakarya, Turkey 54040