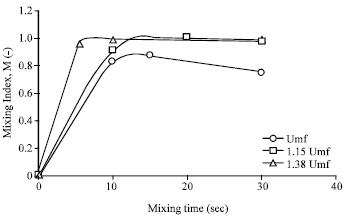
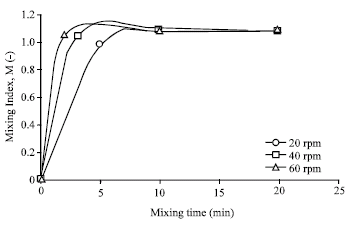
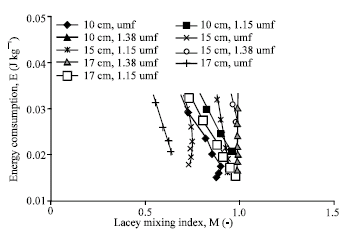
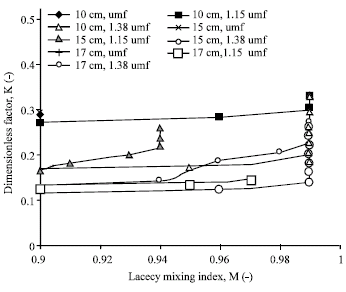
Research Article
Experimental Study on the Mixing of Binary Polymer Particles in Different Types of Mixer
Department of Chemical and Process Engineering, Faculty of Engineering, Universiti Kebangsaan, Malaysia, 43600 Bangi, Selangor, Malaysia
Siti Masrinda Tasirin
Department of Chemical and Process Engineering, Faculty of Engineering, Universiti Kebangsaan, Malaysia, 43600 Bangi, Selangor, Malaysia
Wan Ramli Wan Daud
Department of Chemical and Process Engineering, Faculty of Engineering, Universiti Kebangsaan, Malaysia, 43600 Bangi, Selangor, Malaysia