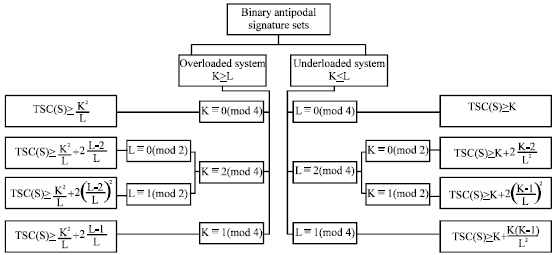
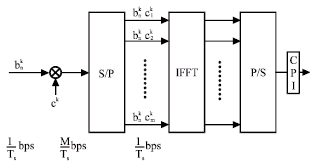
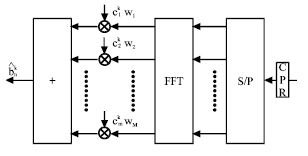
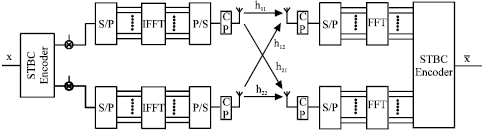
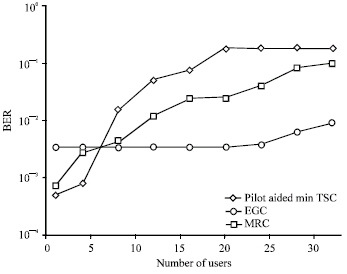
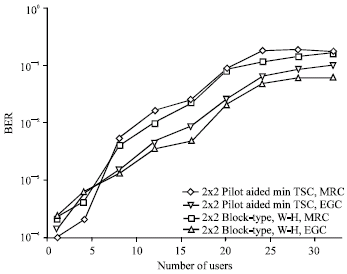
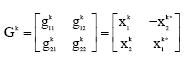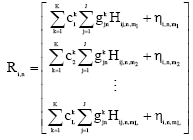Research Article
Overloaded Minimum Total Squared Correlation Signatures Based Pilot Aided System for MC-CDMA and STBC MC-CDMA
School of Engineering and Information Technology Universiti Malaysia Sabah Locked Bag No. 2073 88999 Kota Kinabalu, Sabah, Malaysia
A. Chekima
School of Engineering and Information Technology Universiti Malaysia Sabah Locked Bag No. 2073 88999 Kota Kinabalu, Sabah, Malaysia
M.Y. Hamid
School of Engineering and Information Technology Universiti Malaysia Sabah Locked Bag No. 2073 88999 Kota Kinabalu, Sabah, Malaysia
L. Barukang
School of Engineering and Information Technology Universiti Malaysia Sabah Locked Bag No. 2073 88999 Kota Kinabalu, Sabah, Malaysia
D.V. Viswacheda
School of Engineering and Information Technology Universiti Malaysia Sabah Locked Bag No. 2073 88999 Kota Kinabalu, Sabah, Malaysia