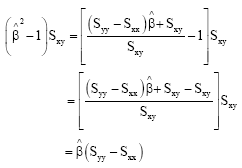
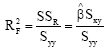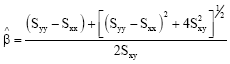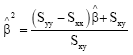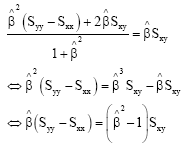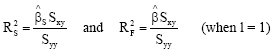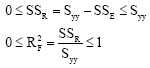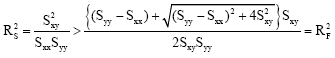Research Article
An Investigation of Causation: The Unreplicated Linear Functional Relationship Model
Faculty of Engineering, Multimedia University, 63100 Cyberjaya, Selangor, Malaysia
Abdul Ghapor Hussin
Centre for Foundation Studies in Science, University of Malaya, 50603 Kuala Lumpur, Malaysia
Omar Mohd Rijal
Institute of Mathematical Sciences, University of Malaya, 50603 Kuala Lumpur, Malaysia