Research Article
Characterization of Decomposed Convex Components of Water Bodies
Science and Technology Research Institute for Defence (STRIDE), Ministry of Defence, Malaysia
Convexity is considered as one of the basic descriptors of shapes. Convexity in image processing has been studied for quite some time (Valentine, 1964; Stern, 1989; Boxer, 1993; Held and Abe, 1994; Popov, 1996; Zunic and Rosin, 2004; Rosin and Mumford, 2004; Rahtu et al., 2004, 2006; Kolesnikov and Franti, 2005; Varosanec, 2007) and has numerous applications, including shape decomposition (Latecki and Lakämper, 1999; Rosin, 2000), camouflage breaking (Tankus and Yeshurun, 2000), object indexing (Latecki and Lakämper, 2000), measurement of border irregularities measurement in medical image analysis (Lee et al., 2003), handwritten word recognition (Kapp et al., 2007) and estimation of derivatives of holomorphic functions (Li, 2007).
An object P is said to be convex if it has the following property: If points A and B belong to P, then all points from the line segment [AB] belong to P as well. The smallest convex set which includes P is called the convex hull of P and is denoted as CH(P). The convexity measure C(P) is defined to be:
| (1) |
In previous research efforts (Dinesh and Pathmanabhan, 2007a, b; Dinesh, 2007a, b), the characterization of the convexity of water bodies was performed by first computing the convex hulls of the corresponding water bodies. In Dinesh and Pathmanabhan (2007a and b), a fractal power law relationship is observed between the convexity measures and areas of water bodies. Convex hull computation increases the sizes of water bodies. This enlargement is not even; smaller water bodies undergo smaller enlargements compared to larger water bodies and hence, convex hull computation alters the water body size distribution. The computed convex hulls have a more even shapiness index distribution compared to the water bodies, as the water bodies are random chaotic objects while convex hulls are well defined polygons. Convex hull computation also causes a loss of homotopic information. In Dinesh (2007a,b), a fractal power law relationship is observed between the average convexity measures of the simulated droughts/floods of water bodies and the level of droughting/flooding. The scaling exponent of this power law, which was named as a fractal dimension, indicates the rate of change of the convexity of water bodies over varying levels of droughting/flooding.
In this research, water body characterization is performed by decomposing water bodies into convex components using the morphological decomposition (Pitas and Venetsanopoulos, 1990). These decomposed convex components are employed to compute the fractal dimensions of the water bodies.
MATHEMATICAL MORPHOLOGY
Mathematical morphology is a branch of image processing that deals with the extraction of image components that are useful for representational and descriptional purposes. The fundamental morphological operators are discussed in Matheron (1975), Serra (1982) and Soille (2003). Morphological operators generally require two inputs; the input image A, which can be in binary or grayscale form and the kernel B, which is used to determine the precise effect of the operator.
Dilation sets the pixel values within the kernel to the maximum value of the pixel neighbourhood. The dilation operation is expressed as:
| (2) |
Erosion sets the pixels values within the kernel to the minimum value of the kernel. Erosion is the dual operator of dilation:
| (3) |
where Ac denotes the complement of A and B is symmetric with respect to reflection about the origin.
An opening (Eq. 4) is defined as an erosion followed by a dilation using the same kernel for both operation. Binary opening preserves foreground regions that have a similar shape to this kernel, or that can completely contain the kernel, while eliminating all other regions of foreground pixels.
| (4) |
Morphological reconstruction allows for the isolation of certain features within an image based on the manipulation of a mask image X and a marker image Y. It is founded on the concept of geodesic transformations, where dilations or erosion of a marker image are performed until stability is achieved (represented by a mask image) (Vincent, 1993).
The geodesic dilation, δG used in the reconstruction process is performed through iteration of elementary geodesic dilations, δ(1), until stability is achieved.
| (5) |
The elementary dilation process is performed using a standard dilation of size one followed by an intersection.
| (6) |
The operation in equation 6 is used for elementary dilation in binary reconstruction. (Vincent, 1993).
Morphological reconstruction is a useful filtering tool. Figure 1a shows an image with circles of various sizes. In order to filter the smaller sized circles, first opening is performed using a square kernel of size 30. The circles that are unable to completely contain the kernel are removed, while the shape of remaining circles is altered (Fig. 1b). Morphological reconstruction is implemented with Fig. 1a being the mask and Fig. 1b being the marker. This restores the original shape of the remaining circles (Fig. 1c). This process is known as opening by reconstruction.
Morphological decomposition (Pitas and Venetsanopoulos, 1990) is a shape representation algorithm that decomposes 2D binary objects into convex components. Each convex component is a subset of the given object and the union of all such components returns the original object. The morphological decomposition of an object into a union of convex components is performed in the following way. The set of maximal inscribable convex components in the object A, that have maximum radius, is found.
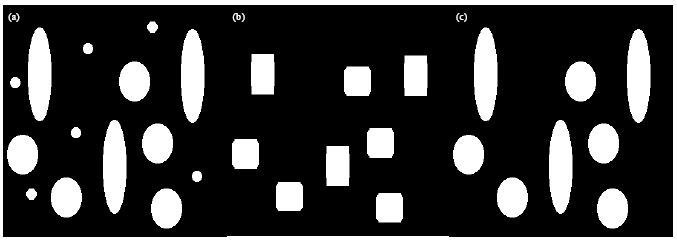 | |
| Fig. 1: | The application of morphological reconstruction in filtering. (a) The original image. (b) The opened image and (c) The reconstructed image |
This set is obtained in the following way. The first set of decomposition is subtracted from the object. The set of maximal inscribable disks in the remaining radius, is found. This set is the second cluster of the decomposition. The first and second sets of the maximal inscribable disks are subtracted from the object and the procedure is repeated until the remainder of the object is an empty set. The whole procedure can be described using the following recursive process:
| (7) |
| (8) |
| (9) |
where ni denotes the number of iterations of erosion and dilation required for the object A-A’I-1 to become an empty set.
CHARACTERIZATION OF DECOMPOSED CONVEX COMPONENTS OF WATER BODIES
Figure 2 shows a number of water bodies of varying shape and sizes situated in the flood plain region of Gothavary River, India. The water bodies were traced from IRS 1D remotely sensed data. Due to the impracticalities of dealing with incomplete water bodies, only the complete water bodies are considered (Fig. 3). A total of 67 distinct individual water bodies (Fig. 4) are identified using the connected component labeling algorithm proposed in Pitas (1993).
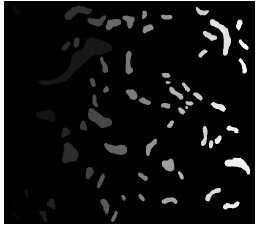
Morphological decomposition is implemented on the water bodies using a size 3 disk kernel. The rate of decay of the water bodies into convex components of decreasing size (Fig. 5) depends on the area and geometric organization of the water bodies. The decomposed convex components of the water bodies are shown in Fig. 6. The union of the decomposed convex components is shown in Fig. 7, where each category of convex components is assigned with different grey levels.
The decomposition of the water bodies into convex components allows for the possibility to represent water bodies of varying shapes and sizes as unions of simple objects. It is observed that more number of smaller size category convex components exists in the water bodies compared to larger convex components. In order to characterize the size distribution of the decomposed convex components, opening by reconstruction is implemented iteratively on the convex components using square kernels of increasing sizes. In each iteration, opening removes convex components that are unable to completely cover the kernel, while modifying the shape of the remaining convex components. The reconstruction step returns the original shape of the remaining convex components.
 | |
| Fig. 2: | Water bodies traced from IRS 1D remotely sensed data |
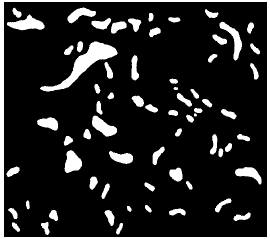 | |
| Fig. 3: | The water bodies after removal of incomplete water bodies |
 | |
| Fig. 4: | Identification of the individual water bodies using connected component labeling. The water body count number is determined by the grey level; the brighter the grey level, the larger the water body number |
 | |
| Fig. 5: | The evolution of decay of the water bodies into convex components of deceasing size |
 | |
| Fig. 6: | The decomposed convex components of the water bodies |
 | |
| Fig. 7: | The union of the decomposed convex components of the water bodies |
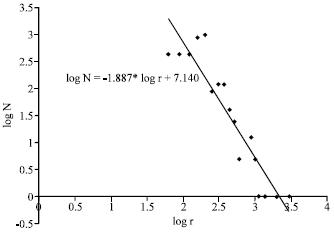 | |
| Fig. 8: | Log-log plot of the number of decomposed convex components removed in each iteration of opening by reconstruction N against the kernel size r |
A log-log plot of the number of convex components removed in each iteration of opening by reconstruction N against the kernel size r is drawn (Fig. 8). A power law relationship is observed between the two parameters:
| (10) |
| (11) |
where 7.140 is a constant of proportionality c and 1.887 is the fractal dimension of the water bodies D, which indicates the measure of complexity of the self-similarity of the water body. This power law relationship is consistent with the decomposition power law relationships derived in Manna and Hermann (1991), Dodds and Weitz (2001 and 2003), Teo et al. (2004), Radhakrishnan et al. (2004), Sagar and Chockalingam (2004) and Chockalingam and Sagar (2005).
| Table 1: | The computed fractal dimensions of the individual water bodies |
 | |
The iterative opening by reconstruction process is implemented on the individual water bodies. The fractal dimension of each individual water body is the slope of the log-log plot of N against r for the corresponding water body. The computed fractal dimensions for the individual water bodies are shown in Table 1.
This approach to fractal dimension computation takes only into account the internal regions of the water bodies, while discarding the non-water body regions. As the number and size distribution of the decomposed convex components depend on the shape of the water bodies, the computed water body fractal dimensions are shape dependant.
In this research, the characterization of the decomposed convex components of water bodies was performed. Morphological decomposition was used to decompose water bodies into convex components. Opening by reconstruction was implemented on the decomposed convex components using square kernels of increasing sizes. A power law relationship was observed between the number of decomposed convex components removed in each iteration of opening by reconstruction and the kernel size. The scaling exponent of this power law is the fractal dimension of the water bodies, which indicates the measure of complexity of the self-similarity of the water bodies. The iterative opening by reconstruction process was implemented on the individual water bodies to compute their fractal dimensions. The computed fractal dimensions are shape dependant and consider the topological regions of water bodies rather than their geometric boundaries.