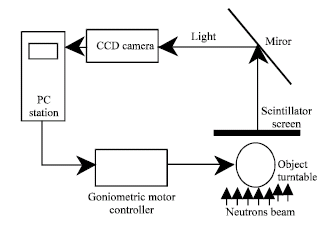
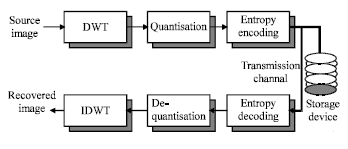
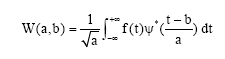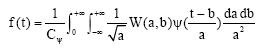Research Article
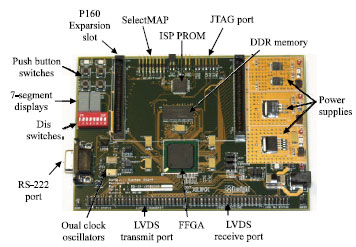
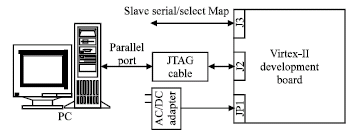
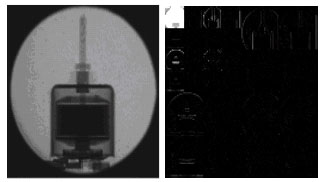
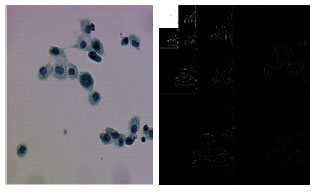
FPGA Implementation of 2D Signals Encoder Using QMF Based Dyadic DWT: Application to Neutron Tomography Projections
Nuclear Research Centre of Birine (CRNB), BPI 80, AinOussera, 17200, Algeria
M. Touiza
Nuclear Research Centre of Birine (CRNB), BPI 80, AinOussera, 17200, Algeria
A. Guessoum
University Saad Dahleb of BLIDA, Signal Processing and Imaging Laboratory (LATS]), Route de Soumaa B.P. 270 BL]DA 09000, Algeria