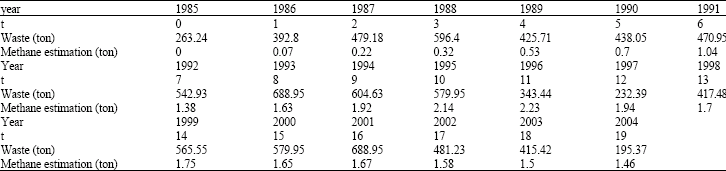
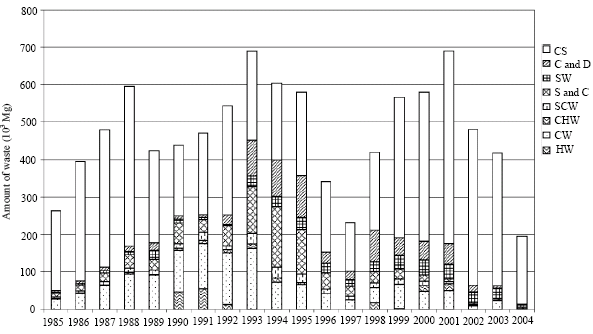
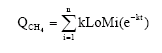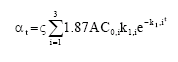Research Article
Applying Simple Numerical Model to Predict Methane Emission from Landfill
Geo environmental Engineering, Iranian University of Science and Technology, Tehran, Iran
Mohammad Reza Sabour
Civil and Environmental Engineering, K.N. Toosi University of Technology, Tehran, Iran
Hamidreza Kamalan
Civil and Environmental Engineering, K.N. Toosi University of Technology, Tehran, Iran
Arash Mansouri
Geo technical Engineering, Iranian University of Science and Technology, Tehran, Iran
Mostafa Abolfazlzadeh
Civil and Environmental Engineering, University of Tehran, Tehran, Iran