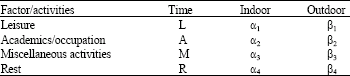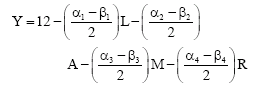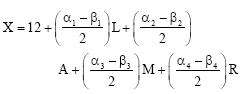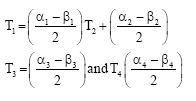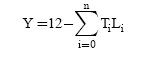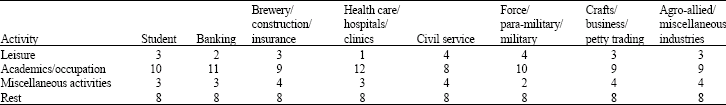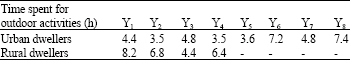Research Article
Occupancy Factor Model for Exposure to Atmospheric Radiation by Urban and Rural Dwellers in Nigeria
Department of Physics, Federal University of Technology, P.M.B, 704, Akure, Nigeria
A.S. Adekola
Department of Physics, Federal University of Technology, P.M.B, 704, Akure, Nigeria