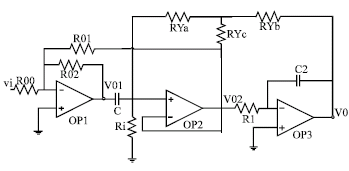
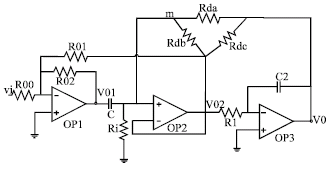
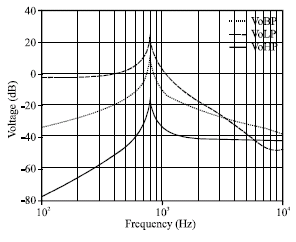
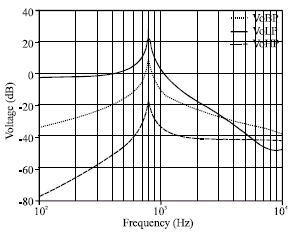
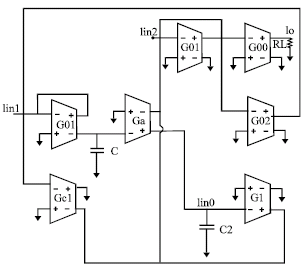
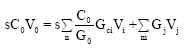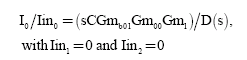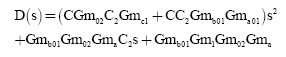Research Article
Design of Current-Mode Gm-C Filters from the Transformation of Opamp-RC Filters
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840, Mexico
Esteban Tlelo-Cuautle
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840, Mexico
Carlos Sanchez-Lopez
UAT. Department of Electronics, Tlaxcala, Mexico