Research Article
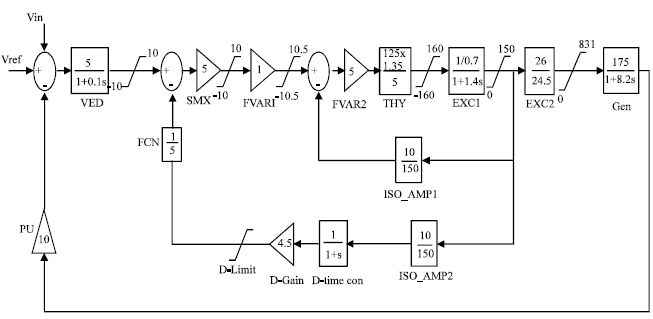
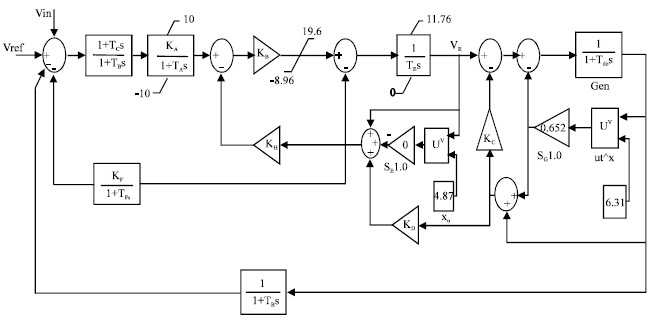
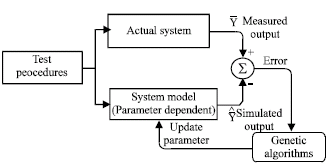
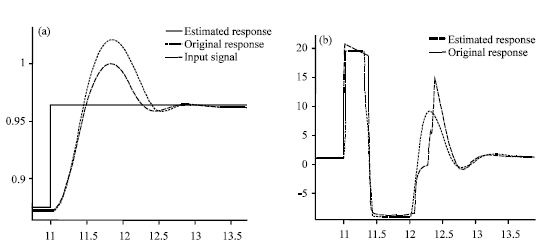
Simulation Model of Brushless Excitation System
College of Electric and Electronics Engineenng, Huazhong University of Science and Technology, Wuhan 430074, China
Afaneen Anwar
Department of Electric and Electronics Engineering, University Technology, Baghdad, Iraq