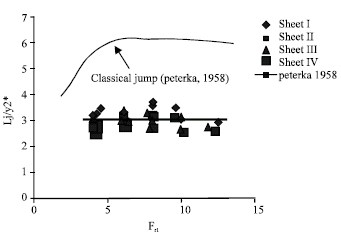
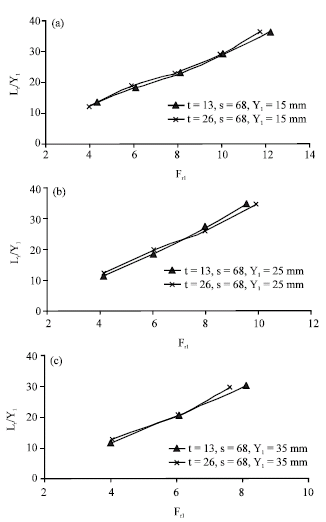
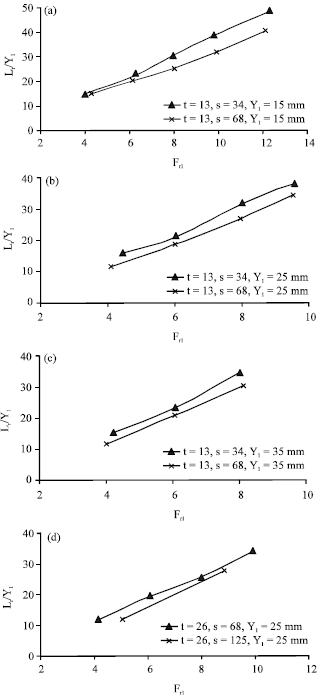
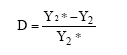Research Article
Corrugated Bed Hydraulic Jump Stilling Basin
Department of Hydraulic Structures, College of Water Science Engineermg, Shahid Chamran University, Ahwaz, Iran
Mahmood Shafai-Bejestan
Department of Hydraulic Structures, College of Water Science Engineermg, Shahid Chamran University, Ahwaz, Iran