Dynamic Analysis of Wind Generators

Wind power does not make any pollution and it also create a recyclable energy. The wind blade speeds significantly affect the measured output power. It is necessary to keep the wind blade tip speed to obtain maximum power. The wind blade speeds significantly affect the energy losses and the power coefficients. It is required to keep the wind blade tip speed to obtain the maximum power coefficient and minimum energy loss. The dynamic problems of the wind turbine generators are formulated by employing the differential quadrature method. The Euler-Bernoulli beam model is used to characterize the wind turbine generator blade. The differential quadrature method is used to transform the partial differential equations that present the dynamic behavior of the wind turbine generator blades into a discrete eigenvalue problem. The results show that the rotation speed could affect the frequencies of the wind generators. The inclined angle could not affect the frequencies of the wind generators significantly.

INTRODUCTION

Renewable resources, such as wind, are replaced continuously by nature. Electrical energy is a form of secondary energy and is derived from primary energy by using wind power. Wind velocities change with time and this inconstancy causes the difficulties to utilize wind power efficiently. Spee et al. (1995) presented a novel control strategy for a bruless doubly fed machine applied to variable speed wind power generation systems. Song and Dhinakaran (1999) explored the nonlinear wind turbine control method. In the design of wind turbine generator, fiber reinforced composites materials have been used. The wind turbine generator composite material in blade applications has stimulated a considerable amount of study. Storti and Aboelnaga (1987) studied the transverse deflections of a straight tapered symmetrical beam attached to a rotating hub as a model for the bending vibration of blades in turbo-machinery. Wagner (1967) calculated the forced vibration response of subsystems attached to a foundation with finite stiffness or mass. Schultz and Tsai (1968) presented data concerning the dynamic material behavior in a glass-filament reinforced epoxy composite. Abarcar and Cunniff (1972) presented the fiber orientation effect on the vibration mode in cantilever beams made of unidirectional fiber reinforced composite materials. Shiau et al. (1996) investigated the vibration and optimum design of a rotating laminated blade subject to constraints on the dynamic behavior. Rand and Barkai (1997) presented a nonlinear formulation for the structural behavior of initially twisted solid and thin walled composite blades. Surace et al. (1997) presented the analysis of the model characteristics of straight, pre-twisted non-uniform blades. Lekhnitskii (1963) solved the static response of an orthotropic composite beam subjected to the simultaneous action of an applied bending moment and an applied torque.

The dynamic characteristics of wind turbine generator composite blades are important in high-speed wind turbine generator designs. The determination of the dynamic characteristics for wind composite blades is one of the great importances. In this study the differential quadrature method is employed to formulate the eigenvalue problem of wind turbine generator composite blade in matrix form. The integrity and computational efficiency of the differential quadrature method in this problem will be demonstrated through a series of case studies.

MAXIMUM POWER OF WIND GENERATORS

Figure 1 shows the geometry of the wind generator. The wind turbine blades are manufactured from carbon fiber laminated composite. The measurements are acquired analog through multi-channel analog to digital circuit. The measured data are stored digitally in the computer. The shaft torque is measured via a strain gauge transducer. The wind generator has three wind composite blades. The wind mechanical power P_w is expressed by

(1)

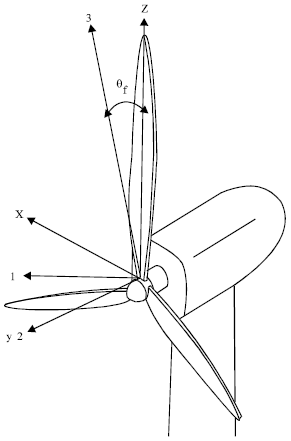Fig. 1:	Geometry of a wind generator

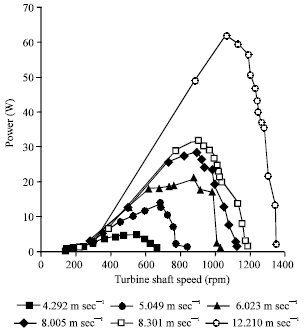Fig. 2:	The output power of the wind generator for various wind speeds

where C_wl is the wind energy loss constant, J is the turbine moment of inertia, ω is the turbine angular speed and P_m is the turbine mechanical power. The turbine mechanical power P_m is expressed by

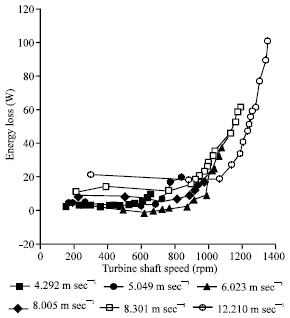Fig. 3:	The energy losses of the wind generator for various wind speeds

Fig. 4:	The power coefficients of the wind generator for various wind speeds

(2)

where T is the torque, C_ml is mechanical energy loss constant. The wind turbine generator power P_e is expressed by

(3)

where ρ_a is the air density, C_p is the rotor efficiency of the turbine, v_w is wind speed and r is wind turbine radius.

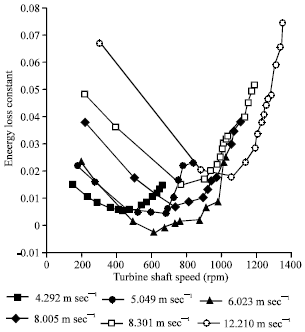Fig. 5:	The energy loss constants of the wind generator for various wind speeds

The air density dependents on the pressure and temperature of the air. Figure 2 shows the measured power of the wind generator for various wind speeds. The results show that the wind blade speeds significantly affect the measured output power. It is needed to keep the wind blade tip speed to obtain maximum power. Figure 3 displays the measured energy losses of the wind generator for various wind speeds. The results show that the wind blade shaft speeds significantly affect the energy losses. The energy losses depend on the rotation speeds of the wind generator. Figure 4 illustrates the measured value of the power coefficient C_p. The results show that the wind blade speeds significantly affect the measured value of the power coefficient C_p. The power coefficient C_p is a function of the wind blade speed. It is necessary to keep the wind blade tip speed to obtain the measured value of the maximum power coefficient C_p. Figure 5 reveals the energy loss constants of the wind generator. There is a local minimum energy loss constant for the wind generator under each wind speed.

DYNAMIC BEHAVIOR OF WIND GENERATORS

The wind blades are attached to a rigid hub. A model for the wind turbine generator composite blade with a rigid hub is assembled. Axes 1, 2 and 3 are the global axes and axes x, y and z are the local blade axes. θ_f is the fiber orientation and θ_i is the inclined angle of the blade. The kinetic energy of the rotating wind composite blades can be derived as

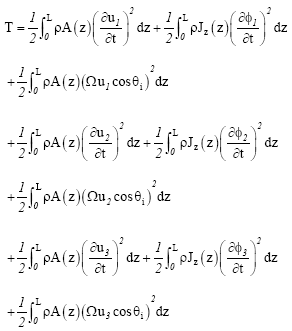(4)

The corresponding strain energy of the rotating wind blades is

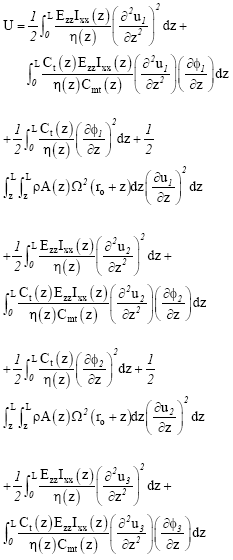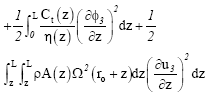(5)

where u₁(z,t) is the displacement of the first blade and φ₁(z,t) is the twist angle of the first blade. u₂(z,t) is the displacement of the second blade and φ₂(z,t) is the twist angle of the second blade. u₃(z,t) is the displacement of the third blade and φ₃(z,t) is the twist angle of the third blade. For the wind turbine generator composite blades, the parameters used in the above equations are defined as

(6)

(7)

(8)

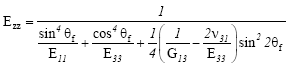(9)

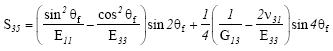(10)

(11)

(12)

where b(z) and h(z) denote respectively the breadth and thickness of the blade. E₁₁ and E₃₃ are Young<’s moduli in 1 and 3 axes, v₃₁ is the Poisson<’s ratio, G₁₃, G₁₂ and G₂₃ are shear moduli in 1-3, 1-2 and 2-3 planes, respectively. With considering the internal and external damping effects in the wind turbine generator composite blade, the virtual work δW in the blade can be derived as:

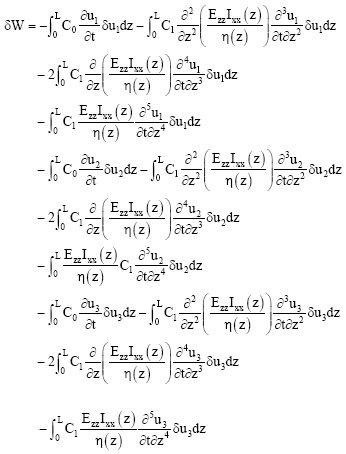(13)

with

(14)

(15)

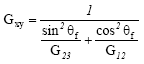(16)

where Ω is the rotation speed of the hub, J_z is the polar moment of inertia, ρ is the density of the material, r₀ is the radius of the hub. C₀ and C₁ are the external and the internal damping coefficients of the wind composite blades, respectively. Substituting Eqs. (4), (5) and (13) into Hamilton equation

(17)

This leads to the equations of motion of the wind turbine generator composite blades as

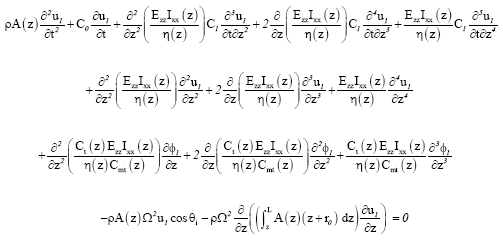(18)

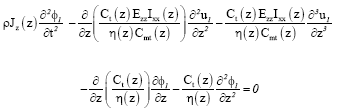(19)

(20)

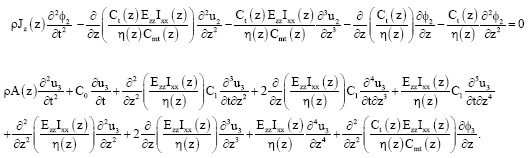(21)

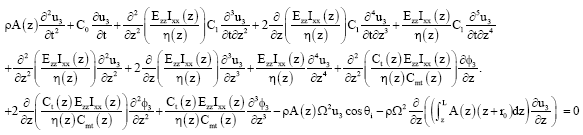(22)

(23)

The corresponding boundary conditions are

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

Consider u₁(z,t) = U₁ (z)e^λt, φ₁ (z,t) = φ₁ (z)e^λt, u₂ (z,t) = U₂ (z)e^λt, φ₂ (z,t) = φ₂ (z)e^λt, u₃ (z,t) = U₃ (z)e^λt and φ₃ (z,t) = φ₃ (z)e^λt, the governing equations for the wind turbine generator blades can be rewritten as

(42)

(43)

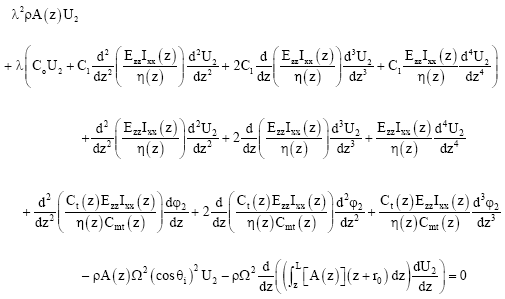(44)

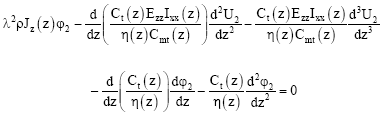(45)

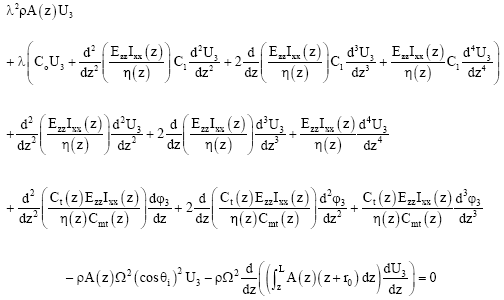(46)

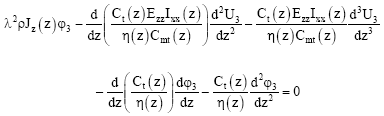(47)

The corresponding boundary conditions are

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

(65)

THE DIFFERENTIAL QUADRATURE METHOD

One of the fields among which one can find extensive differential quadrature method applications is structural mechanics. Han and Liew (1999) analyzed annular plates using the differential quadrature method. Striz et al. (1994) used the quadrature element method for static analysis. Du et al. (1996) used the differential quadrature method for buckling analysis. Quan and Chang et al. (1989a, 1989b) derived the weighting coefficients in a more explicit way. The basic concept of the differential quadrature method is that the derivative of a function at a given point can be approximated as a weighted linear sum of the functional values at all of the sample points in the domain of that variable. Using this approximation, the differential equation is then reduced into a set of algebraic equations. The number of equations depends on the selected number of sample points within the domain. As for any polynomial approach, the accuracy of the solution in this method may be improved by increasing the number of sample points. Possible oscillations in the numerical results arising from higher order polynomials can be avoided by using numerical interpolation methods. Suppose that there are N sample points in the domain. For a function f(z), differential quadrature method approximation for the mth order derivative at the sample point z_i is given by

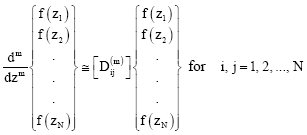(66)

where f(z_i) is the functional value at the sample point z_i and D_ij^(m) are the weighting coefficients of the mth order differentiation attached to these functional values.

In order to determine the weighting coefficients D_ij^(m) and to overcome the numerical ill-conditions in determining the weighting coefficients D_ij^(m), a Lagrangian interpolation polynomial was introduced by Quan and Chang (1989a, 1989b), which is

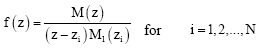(67)

where

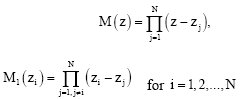Substituting Eq. (67) into Eq. (66) leads to

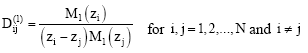(68)

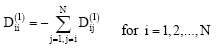(69)

Once the sample points are selected, the coefficients of the weighting matrix can be obtained from equations (68) and (69).

The most convenient method is to peak up the sample points in an equal space sample point distribution. The selection of sample points always plays an important role (Bert et al., 1994; Malik and Bert, 1996) in the solution accuracy of the differential quadrature method. Poor accuracy results were obtained using this equally spaced distribution. An unequally spaced sample point distribution, i.e., Chebyshev-Gauss-Lobatto distribution (Bert et al., 1994; Malik and Bert, 1996), has been used to improve the calculation accuracy. The unequally spaced inner points of each blade using the Chebyshev-Gauss-Lobatto distribution in the present computation are distributed as

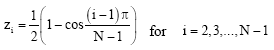(70)

The boundary points of the clamped-free wind turbine generator composite blades in this computation are defined as

(71)

(72)

The differential quadrature weighting coefficients of second-, third- and fourth-order derivatives in the differential quadrature method, D_ij⁽²⁾, D_ij⁽³⁾ and D_ij⁽⁴⁾ may be computed by (Bert et al., 1994; Malik and Bert, 1996).

(73)

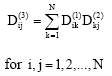(74)

(75)

By employing the differential quadrature method, Eq. (66) is substituted into equations (42)-(47). The equations of motion for the wind turbine generator composite blades can be rearranged in matrix form as

(76)

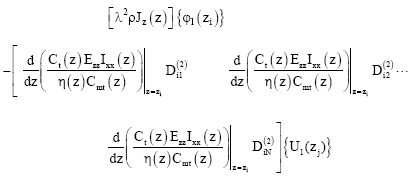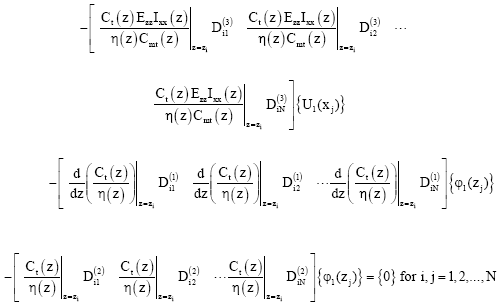(77)

(78)

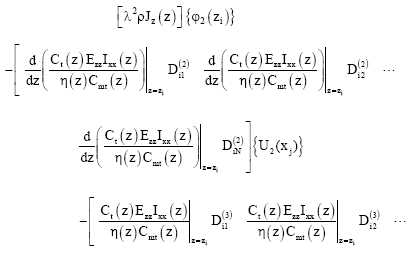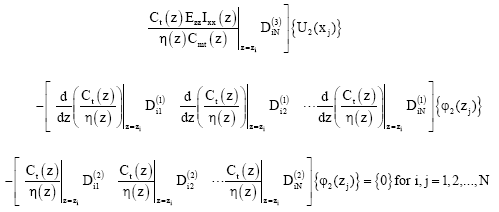(79)

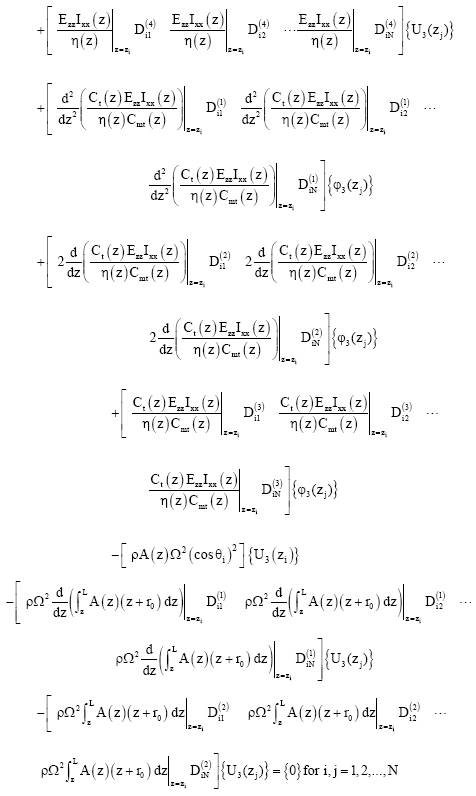(80)

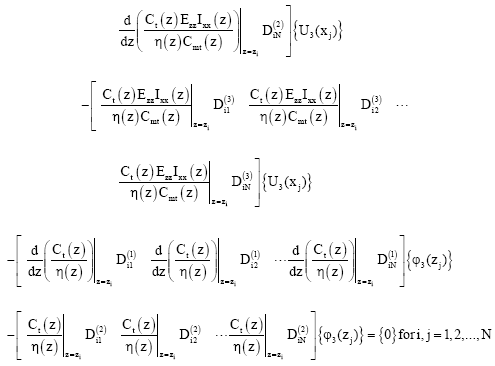(81)

(82)

According to the differential quadrature method, boundary condition equations (48)-(65) take the following discrete forms:

(83)

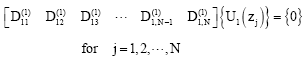(84)

(85)

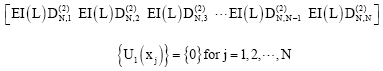(86)

(87)

(88)

(89)

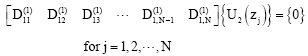(90)

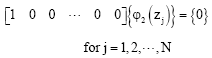(91)

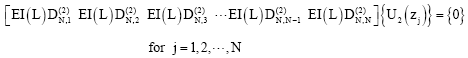(92)

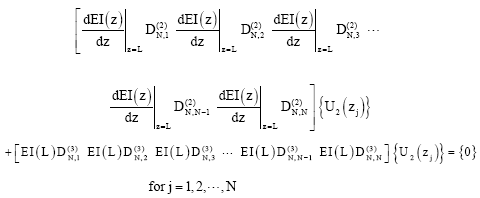(93)

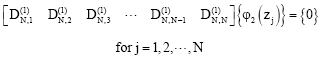(94)

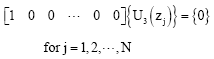(95)

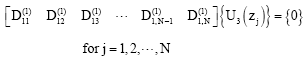(96)

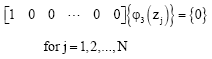(97)

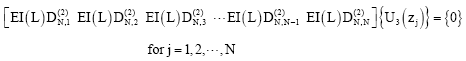(98)

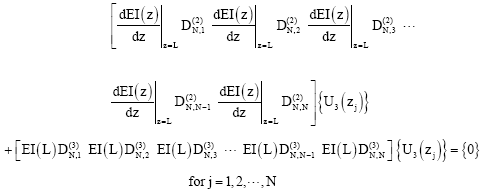(99)

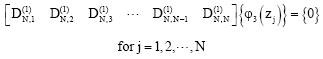(100)

Fig. 6:	The frequencies of the wind generator for various wind speeds

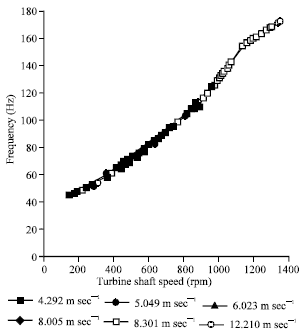
Fig. 7:	The frequencies of the wind generator for various rotation speeds

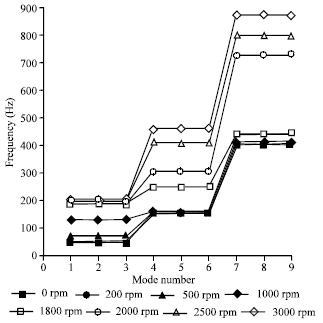
Fig. 8:	The frequencies of the wind generator for various inclined angles

Figure 6 illustrates the frequencies of the wind generator for various wind speeds. The material properties and the geometric dimensions of the wind composite blade are given as: G₁₂ = 2.542 GPa, E₁₁/G₁₂ = 3.7, G₂₃ = 4.305 GPa, E₃₃/G₂₃ = 30, G₁₃ = 5.158 GPa, v₃₁ = 0.3, r₀ = 5.5 cm, θ_f = 0.0, L = 52.5 cm and ρ = 1550 kg m^-3. The results reveal that the frequencies of the wind generator are strongly dependent on the blade shaft speed. The frequencies of the wind generator keep increasing with increasing the rotation speeds. Results indicate that the wind speeds are not the key factors to affect the natural frequencies of the wind generator. Figure 7 displays the frequencies of the wind generator for various rotation speeds. Numerical results in this example reveal that the frequencies of the wind generator might be affected by the rotation speed. Figure 8 shows the frequencies of the wind generator for various inclined angles θ_i. The numerical results show that the inclined angle θ_i has not great effect on the frequencies of the wind generator.

CONCLUSIONS

Due to the coupling effect of torsion and flexure in the wind turbine composite blades, the dynamic characteristics of the wind turbine generator composite blades are much more complicated than the wind turbine isotropic blades. The wind blade speeds significantly affect the measured output power. It is possible to maintain optimal energy generation by tracking the wind speed changes and wind blade shaft speeds. The wind blade shaft speeds significantly affect the energy losses and the power coefficients. Numerical results in this study show that the rotation speed could affect the frequencies of the wind generator seriously. Numerical results in this study showed that the inclined angle could not affect the frequencies of the wind generators gravely. The formulation presented in this article reveals that the differential quadrature method is convenient for solving problems governed by fourth or higher order differential equations. The simplicity of this formulation makes its own good candidate for modeling more complicated applications.