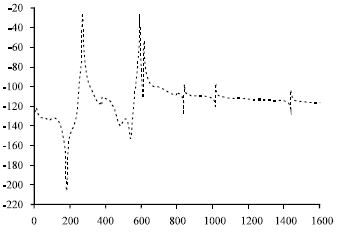
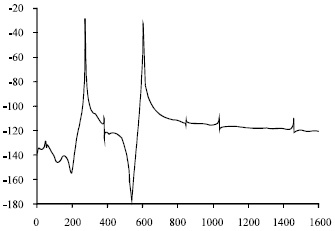
Research Article
Analysis of Crankshafts Vibrations to Compare the Dynamic Behavior of Steel and Cast Iron Crankshafts
Department of Bio-System Engineering, University of Tehran, Iran
H. Afshari
Department of Bio-System Engineering, University of Tehran, Iran
H. Mobli
Department of Bio-System Engineering, University of Tehran, Iran