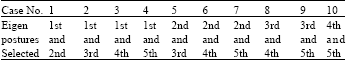Research Article
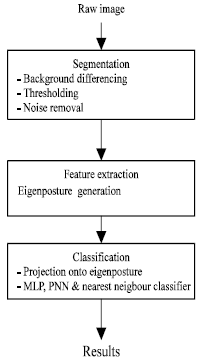
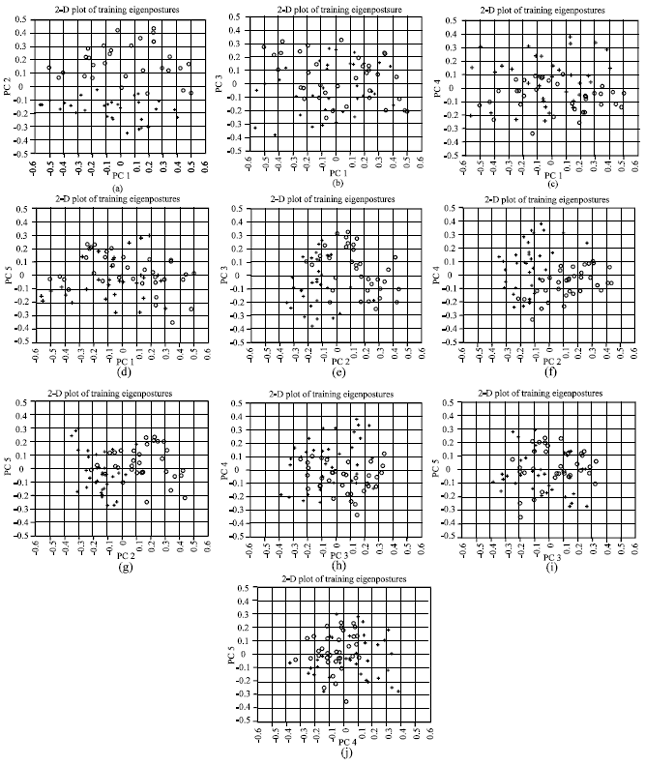
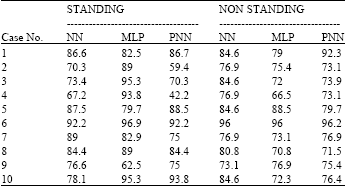
Eigenposture for Classification
Department of Electrical, Electronics and Systems, Faculty of Engineermg, Signal Processing Research Group, Universiti Kebangsaan Malaysia 43600 EXM Bangi, Selangor DE, Malaysia
Aini Hussain
Department of Electrical, Electronics and Systems, Faculty of Engineermg, Signal Processing Research Group, Universiti Kebangsaan Malaysia 43600 EXM Bangi, Selangor DE, Malaysia
Salina Abdul Samad
Department of Electrical, Electronics and Systems, Faculty of Engineermg, Signal Processing Research Group, Universiti Kebangsaan Malaysia 43600 EXM Bangi, Selangor DE, Malaysia
Hafizah Husain
Department of Electrical, Electronics and Systems, Faculty of Engineermg, Signal Processing Research Group, Universiti Kebangsaan Malaysia 43600 EXM Bangi, Selangor DE, Malaysia
Mohd Marzuki Mustafa
Department of Electrical, Electronics and Systems, Faculty of Engineermg, Signal Processing Research Group, Universiti Kebangsaan Malaysia 43600 EXM Bangi, Selangor DE, Malaysia