ABSTRACT
In this study, several radial basis function networks are compared according to their approximation ability in time series forecasting problems. Optimal values for the tested parameters are obtained using computer simulation runs. Effects of width selection in Gaussian Kernels, of the number of neurons in the hidden layer, and of selection of kernel function are investigated.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2006.1608.1611
URL: https://scialert.net/abstract/?doi=jas.2006.1608.1611
INTRODUCTION
There are many applications of time series in science and engineering, like electrical load estimation, risk prediction, river flood fore casting, stock market prediction, etc.
For making a prediction using time series, a large variety of approaches are available. Prediction of scalar time-series {x(n)} refers to the task of finding an estimate ![]() of the next future samplex(n+1) based on the knowledge of the history of time-series, i,e, the samples x(n), x(n-1), … (Rank.,2003).
of the next future samplex(n+1) based on the knowledge of the history of time-series, i,e, the samples x(n), x(n-1), … (Rank.,2003).
Linear prediction, where the estimate is based on a linear combination of N past samples can be represented as below:
with the prediction coefficients aj, i = 0,1, … N-1.
Introducing a general nonlinear function f(.): ![]() applied to the vector x(n) = [x(n), x(n - M), …, x(n-(N-1))M]T of past samples, we arrive at the nonlinear prediction approach
applied to the vector x(n) = [x(n), x(n - M), …, x(n-(N-1))M]T of past samples, we arrive at the nonlinear prediction approach
RADIAL BASIS FUNCTION NETWORK
The RBF network consists of 3 layers: An input layer, a hidden layer and an output layer. A typical RBF network is shown in Fig. 1.
Mathematically, the network output for linear output nodes can be expressed as below:
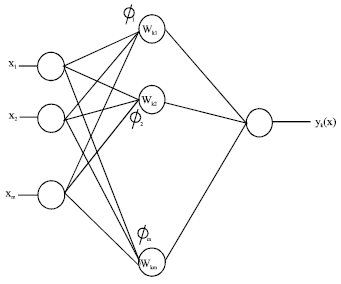 | |
| Fig. 1: | Typical RBF network |
where, x is the input vector with elements xi (where i is the dimension of the input vector); ![]() is the vector to determine the center of the basis function; φj with elements
is the vector to determine the center of the basis function; φj with elements ![]() ; Wkj‘s are the weights and Wko is the bias (Harpham et al., 2006). The basis function φj(-) provides the non-linearity.
; Wkj‘s are the weights and Wko is the bias (Harpham et al., 2006). The basis function φj(-) provides the non-linearity.
BASIS FUNCTIONS
The most used basis functions are Gaussian and multiquadratic functions. They are given below:
Gaussian
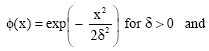 |
Multiquadratic
p is between 0 and 1. Usually p is taken as ½.
CALCULATING THE OPTIMAL VALUES OF WEIGHTS
A very important property of the RBF Network is that it is a linearly weighted network in the sense that the output is a linear combination of m radial basis functions, written as below:
The main problem is to find the unknown weights {W(i)}mi = 1.
For this purpose, the general least squares principal can be used to minimize the sum squared error:
With respect to the weights of f, resulting in a set of m simultaneous linear algebraic equations in the m unknown weights
Where,
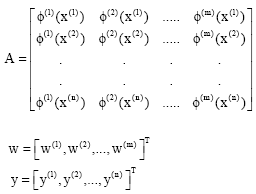 |
In the special case where n = m, the resultant system is just
The output y(x) represents the next value of y in time t taking input values x1, x2, …, xn that represent the previous function values set with values yt-1, yt-2, …, yt-n. So, xn corresponds to yt-1, xn-1 corresponds to yt-2 etc. as in Fig. 2.
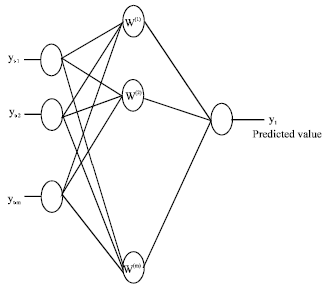 | |
| Fig. 2: | Finding predicted value yt |
SIMULATION RESULTS
Several computer simulation runs are carried out to find the optimal values of parameters in radial basis functions such as width (δ) and centers (![]() ’s).
’s).
The effect of type of radial basis functions (Gaussian, multiquadratic etc.) in function approximation is also investigated.
The last parameter to be investigated is the number of neurons in the hidden layer. The effect of the number of neurons in the hidden layer on performance of neural network for time series prediction is studied.
EFFECT OF WIDTH SELECTION
For this work, the time-series data of American Express Bank is used. Monthly log data consists of 324 data items. The first 162 data items are used for training and the remaining 162 data items are used for forecasting.
Figure 3 shows the results of simulation run with δ = 0.5 and 18 neurons in the hidden layer for the last 50 data items.
In Fig. 4, similar results for δ = 1.2 and 18 neurons in the hidden layer are shown.
For δ = 1.5 and 18 neurons in the hidden layer an optimal solution is obtained with minimum error rate. This result is shown in Fig. 5.
In Fig. 6, for the optimal solution, all the real and predicted values are shown.
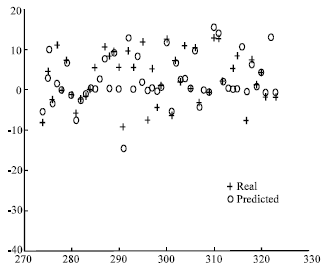 | |
| Fig. 3: | δ = 0.5 and 18 neurons in the hidden layer. Last 50 data items |
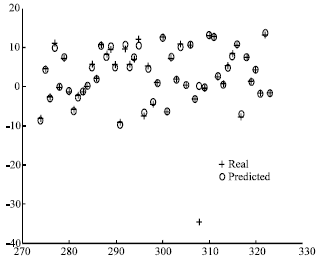 | |
| Fig. 4: | δ = 1.2 and 18 neurons in the hidden layer. Last 50 data items |
 | |
| Fig. 5: | δ = 1.5 and 18 neurons in the hidden layer. Last 50 data items |
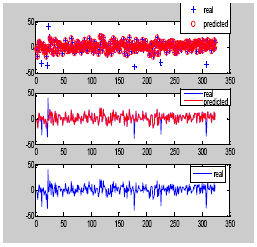 | |
| Fig. 6: | δ = 1.5 and 18 neurons in the hidden layer. Optimal solution |
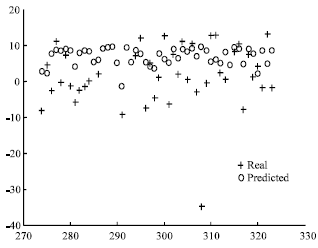 | |
| Fig. 7: | δ = 1.5 and 9 neurons in the hidden layer. Last 50 data items |
As can be seen from simulation results presented above, the width parameter (δ) has an important effect on optimal solution.
EFFECT OF NUMBER OF NEURONS IN THE HIDDEN LAYER
The second important parameter is the number of neurons that are used in the hidden layer of the RBF network.
In Fig. 7, simulation results for δ = 1.5 and 9 neurons in the hidden layer are shown.
If we compare these results with the results that is given in Fig. 5 for δ = 1.5 and 18 neurons in the hidden layer, then we can see big differences between two figures.
If we increase number of number of neurons in the hidden layer while δ remains fixed, then we can obtain better results in the prediction problem.
EFFECT OF KERNEL FUNCTIONS
The effect of the type of kernel function (Gaussian, multivariate etc) is problem dependent, which means it can change from one problem to another.
CONCLUSIONS
In this study, different radial basis function networks are compared according to their ability to predict results in time series forecasting problem.
Optimal values for the tested parameters are obtained using simulation runs. Optimal width value of the Gaussian function is obtained as 1.5 for the data file to be processed and the optimal number of neurons in the hidden layer of RBF network is found as 18 for the same problem.
In future research, the relationships between the statistical parameters of data points (average, standard deviation, etc.) and parameters of the RBF network will be investigated for the optimal solution in time series forecasting problems.
REFERENCES
- Duy, N.M. and T.T. Cong, 2003. Approximation of function and its derivations using radial basis function networks. Applied Math. Modell., 27: 197-220.
Direct Link - Harpham, C. and C.W. Dawson, 2006. The effect of different basis functions on a radial basis function network for time series prediction a comparative study. Neurocomputing, 69: 2161-2170.
Direct Link - Rank, E., 2003. Application of bayesian trained RBF networks to nonlinear time-series modeling. Signal Process., 83: 1393-1410.
Direct Link








