ABSTRACT
The dynamic characteristics of plates with mixed boundary and sprung mass are investigated. The vibration analysis of plates with various boundary conditions and sprung masses is numerically modeled using the differential quadrature method. The differential quadrature method is applied to each region and with the imposition of appropriate boundary conditions and the problem is transformed into a standard eigenvalue problem. The results also demonstrate the efficiency of the method in treating this class of engineering problem.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2006.1463.1471
URL: https://scialert.net/abstract/?doi=jas.2006.1463.1471
INTRODUCTION
Vibration is the most important modes of failure in plates with sprung mass and it plays a crucial role in engineering. Avalos et al. (1993) dealt with the solution of vibration by a simply mounted concentred mass using the well-known normal mode. Xiang et al. (1997) used the Ritz method combined with a variation to solve vibration of rectangular mindlin plates resting on elastic edge supports. Laura and Grossi, (1981) calculated the fundamental frequency coefficient for a rectangular plate with edges elastically restrained against both translation and rotation using polynomial coordinate functions and the Rayleigh-Ritz=s method. Wu and Luo (1997) solved the problem of the natural frequencies and the corresponding mode shapes of a uniform rectangular flat plate carrying any number of point masses and translational springs using the analytical-and-numerical-combined method. Grossi and Nallim (1997) analyzed the problem the strain energy stored in rotational springs at the plate edges of non-uniform thickness using the Rayleigh-Ritz method with a polynomial expression as approximating function. Nicholson and Bergman (1986) used the Green=s function express the natural modes for the damped plate-oscillator systems. Gorman (1997) solved the free vibration problem of shear deformable plates resting on uniform elastic foundations using the modified Superposion-Galerkin method.
This work focuses on the application of differential quadrature method to the vibration of plates with various boundary conditions and sprung masses. In the following section an overview of differential quadrature method to preset the computation of its weighting coefficients offered and discussed the selection problem. The integrity and computational efficiency of the method will be demonstrated through a series of case studies. Very few study in the literature have presented the vibration analysis of rectangular plates with various boundary conditions and sprung masses using the differential quadrature method.
THE DIFFERENTIAL QUADRATURE METHOD
With the increasing use of new fast and affordable computers, along with the availability of various numerical methods, the solutions of several complicated engineering problems have now become efficiently achievable. The finite differences method, the finite element method and the boundary element method have been used extensively for solving linear and nonlinear differential equations and consequently there are several commercially developed software packages. The development of new techniques from the standpoint of computational efficiency and numerical accuracy is of primal interest. The differential quadrature method is originally proposed by Bellman et al. (1972). Since it has been developed, several researchers have applied the differential quadrature method to solve a variety of problems in different fields of science and engineering. The differential quadrature method has been shown to be a powerful contender in solving initial and boundary value problems and become an alternative to the existing methods such as the finite element method or the finite difference method. One of the fields among which can find extensive applications of differential quadrature method is structural mechanics. Civan (1994) solved multivariable mathematical models using differential quadrature method and differential cubature method. Han and Liew (1999) analyzed the axisymmetric free vibration of moderately thick annular plates using the differential quadrature method. Chen and Zhong (1997) pointed out that differential quadrature method and differential cubature method, due to their global domain property, are more efficient for nonlinear problems than the traditional numerical techniques such as finite element method and finite difference method. The differential quadrature method is used analyze the mechanical behavior of anisotropic plates and beams (Bert et al., 1993).
The partial differential equation can be reduced to a set of algebraic equations using the differential quadrature method. Possible oscillations of numerical results arising from higher order polynomials can be avoided by using numerical interpolation methods. The differential quadrature method uses the basis of the Gauss method in deriving the derivative of a function. It follows that the partial derivative of a function with respect to a space variable can be approximated by a weighted linear combination of function values at some intermediate points in that variety. A differential quadrature approximation at the ith discrete point on a grid in the direction of x-axis is given by
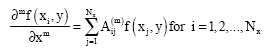 | (1) |
A differential quadrature approximation at the ith discrete point on a grid in the direction of y-axis may be written as
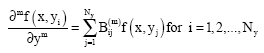 | (2) |
where AIj(m) and Bij(m) are the weighting coefficients.The test function can be written as
| (3) |
Substituting Eq. (3) to Eq. (1) and (2), Eq. (1) and (2) are computed by
| (4) |
and
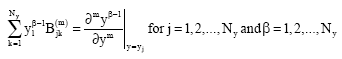 | (5) |
The higher-order derivates may be obtained using following equations
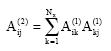 | (6) |
| (7) |
| (8) |
| (9) |
where ![]() are the 1th, 2th, …, mth order weighting coefficient matrix in the direction of x-axis, respectively.
are the 1th, 2th, …, mth order weighting coefficient matrix in the direction of x-axis, respectively.
| (10) |
| (11) |
| (12) |
 | (13) |
where ![]() are the 1th, 2th, …, mth order weighting coefficient matrix in the direction of y-axis respectively. The above relation gives the higher order weighting coefficient matrix based on the first-order derivative weighting coefficients. The above relations are not restricted to the choice of sampling points. It is emphasized that the number of the test functions must be greater than the highest order of derivative in the governing equations.
are the 1th, 2th, …, mth order weighting coefficient matrix in the direction of y-axis respectively. The above relation gives the higher order weighting coefficient matrix based on the first-order derivative weighting coefficients. The above relations are not restricted to the choice of sampling points. It is emphasized that the number of the test functions must be greater than the highest order of derivative in the governing equations.
The selection of locations of the sampling points is important in ensuring the accuracy of the solution of differential equations. Using equally spaced points can be considered to be a convenient and an easy selection method. A more accurate solution could be obtained by choosing a set of unequally spaced sampling points for a domain separate into by Nx and Ny points. A simple and good choice can be the roots of shifted Chebyshev and Legendre points. The inner points are
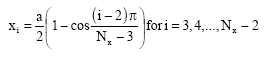 | (14) |
in the direction of x-axis
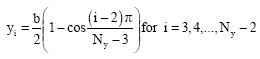 | (15) |
in the direction of y-axis and boundary points are
| (16) |
| (17) |
| (18) |
| (19) |
in the direction of x-axis.
| (20) |
| (21) |
| (22) |
| (23) |
in the direction of y-axis. δx and δy are small distance, a is the length of the plate in the direction of x-axis and b is the length of the plate in the direction of y-axis.
TRANSVERSE VIBRATION OF A RECTANGULAR PLATE AND MASS-SPRING SYSTEM
Figure 1 depicts the geometry of a plate with mass-spring system. The strain energy of the plate and mass-spring system is
 | (24) |
The kinetic energy of the plate and mass-spring system is
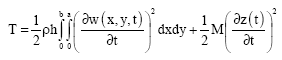 | (25) |
where w is the deflection of the plate, M is the concentrated mass, k is the spring constant, z is the sprung mass location, x0 is the location of sprung mass in the direction of x-axis, y0 is the location of sprung mass in the direction of y-axis, t is the time, D = Eh3/(12(1-v2)) is the flexural rigidity, E is Young=s modulus, ρ is the density of the plate material and h is the plate thickness. Substituting Eqs. (24) and (25) into Hamilton=s equation, this leads to the equations of motion of the plate with sprung mass as:
 | (26) |
| (27) |
 | |
| Fig. 1: | A plate partially rotational spring supported |
At a simply supported or a clamped boundary, the transverse deflection of the plate is zero:
| (28) |
at a simply supported boundary, the condition of zero normal moment can be reduced to
| (29) |
in the direction of x-axis and
| (30) |
in the direction of y-axis. The condition of zero normal moment at a free boundary in the direction of x-axis is given by
| (31) |
where v is Poisson=s ratio. The condition of zero normal moment at a free boundary in the direction of y-axis is given by
| (32) |
The condition of zero effective shear force at a free boundary is given by
| (33) |
in the direction of x-axis and
| (34) |
in the direction of y-axis. The following form gives the condition of spring supported:
| (35) |
in the direction of x-axis and
| (36) |
in the direction of y-axis. kφ is the torsion stiffness. Substituting w = Weiωt and z = Zeiωt into Eq. (26) and (27), Eq. (26) and (27) can be written as
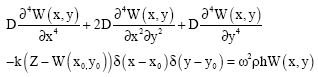 | (37) |
| (38) |
where ω is the natural frequency. Substituting Eq. (1) and (2) to Eq. (37) and (38), leads to
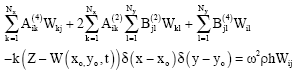 | (39) |
| (40) |
The algorithmic procedure of the differential quadrature method leads to a simply supported or a clamped boundary, the transverse deflection of the plate at a simply supported boundary can be written as
| (41) |
The condition of zero normal moment can be reduced to the following discrete forms. For example, at the edge y = 0
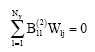 | (42) |
in the direction of y-axis. The condition of zero normal moment at a free boundary can be reduced to the following discrete forms. For example, at the edge y = 0
| (43) |
The condition of zero effective shear force at a free boundary can be reduced to the following discrete forms. For example, at the edge y = 0
| (44) |
The following discrete form gives the condition of spring support. For example, at the edge y = 0
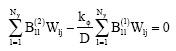 | (45) |
in the direction of y-axis. Eq. (39)-(45) can be rearranged in matrix form as
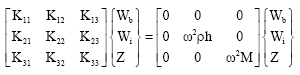 | (46) |
where Kij is the stiffness matrix element, the subscript b and i refer to the locations at the boundary and the interior regions, respectively. The vector {Wb} and {Wi} are the normal deflection vectors corresponding to the boundary and interior points. By substituting Eq. (46) into a general eigenvalue form, Eq. (46) can be expressed as
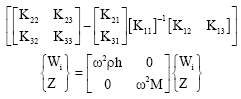 | (47) |
The eigenvalues will be obtained by solving the eigenvalue problem of Eq. (47).
RESULTS AND DISCUSSION
Figure 2 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 0.5 and the uniform equidistant distribution of discrete grid points. The dimensionless natural frequency is defined as ![]() .
.
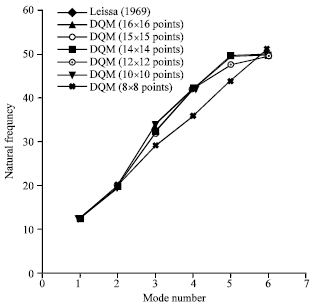 | |
| Fig. 2: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 0.5 and the uniform equidistant distribution of discrete grid points |
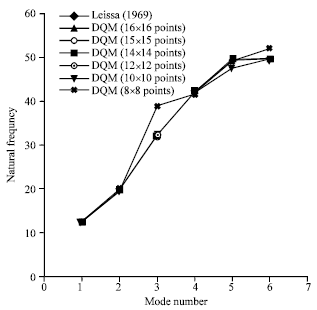 | |
| Fig. 3: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 0.5 with the roots of shifted Chebyshev and Legendre points |
The other results in Figure 2 are cited from reference (Leissa, 1969). It can be seen that the numerical results agree with the data from theory to within 5.38(%) when just 16x16 sample points are used. Figure 3 lists the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 0.5 with the roots of shifted Chebyshev and Legendre points. It can be seen that the numerical results agree with the data from theory to within 4.43(%) when just 10x10 sample points are used.
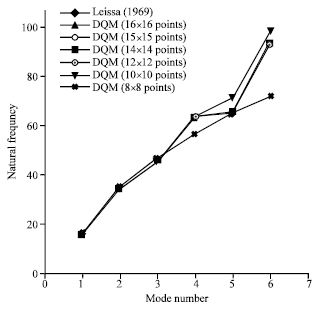 | |
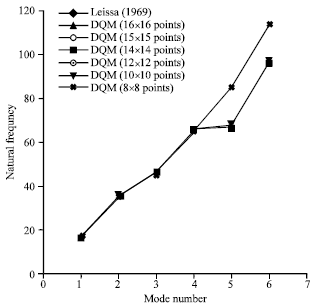
| Fig. 4: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 0.8 and the uniform equidistant distribution of discrete grid points |
 | |
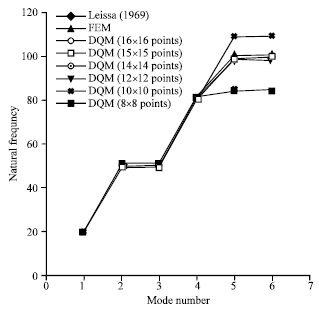
| Fig. 5: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 0.8 and the roots of shifted Chebyshev and Legendre points |
Figure 4 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 0.8 and the uniform equidistant distribution of discrete grid points. It can be seen that the numerical results agree with the data from theory to within 0.50(%) when just 16x16 sample points are used. Figure 5 lists the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 0.8 with the roots of shifted Chebyshev and Legendre points.
 | |
| Fig. 6: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.0 and uniform equidistant distribution of discrete grid points |
 | |
| Fig. 7: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.0 and the roots of shifted Chebyshev and Legendre points |
It can be seen that the numerical results agree with the data from theory to within 0.01(%) when just 12x12 sample points are used.
Figure 6 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.0 and the uniform equidistant distribution of discrete grid points. It can be seen that the numerical results agree with the data from theory to within 0.09(%) when just 16x16 sample points are used.
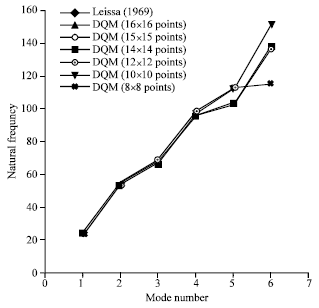 | |
| Fig. 8: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.2 and the uniform equidistant distribution of discrete grid points |
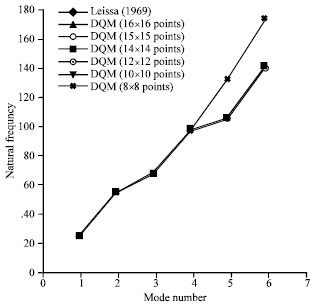 | |
| Fig. 9: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.2 and the roots of shifted Chebyshev and Legendre points |
Figure 7 displays the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.0 with the roots of shifted Chebyshev and Legendre points. It can be seen that the numerical results agree with the data from theory to within 0.01(%) when just 12x12 sample points are used. The computational time for using the differential quadrature method with 8x8, 10x10, 12x12, 14x14, 15x15 and 16x16 sample points are 0.601, 1.423, 11.186, 27.059, 37.474 and 37.484 seconds, respectively.
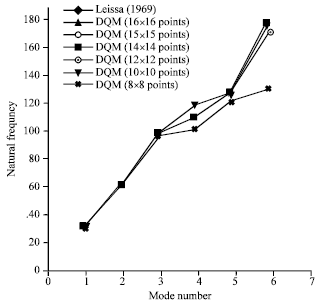 | |
| Fig. 10: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.5 and the uniform equidistant distribution of discrete grid points |
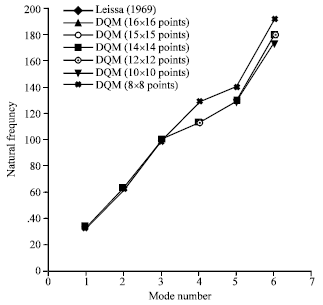 | |
| Fig. 11: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.5 and the roots of shifted Chebyshev and Legendre points |
However, a computational time over 68.659 seconds is required for using FEM in the similar problem.
Figure 8 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.2 and the uniform equidistant distribution of discrete grid points. It can be seen that the numerical results agree with the data from theory to within 0.10(%) when just 16x16 sample points are used.
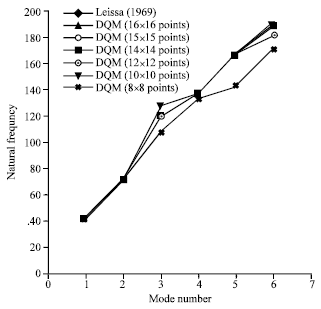 | |
| Fig. 12: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.8 and the uniform equidistant distribution of discrete grid points |
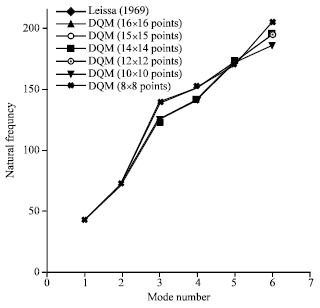 | |
| Fig. 13: | The natural frequencies of the plates which are supported as all of edges are simple support with a/b = 1.8 and the roots of shifted Chebyshev and Legendre points |
Figure 9 displays the eigenvalue of the plates which are supported as all o f edges are simple support with a/b = 1.2 with the roots of shifted Chebyshev and Legendre points. It can be seen that the numerical results agree with the data from theory to within 0.01(%) when just 12x12 sample points are used.
 | |
| Fig. 14: | The natural frequencies of the plates which are a spring-mass system mounted on and supported by simple support with different M/MP |
Figure 10 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.5 and the uniform equidistant distribution of discrete grid points. It can be seen that the numerical results agree with the data from theory to within 7.08(%) when just 10x10 sample points are used. Figure 11 plots the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.5 with the roots of shifted Chebyshev and Legendre points. It can be seen that the numerical results agree with the data from theory to within 3.76(%) when just 10x10 sample points are used.
Figure 12 shows the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.8 and the uniform equidistant distribution of discrete grid points. It can be seen that the numerical results agree with the data from theory to within 4.09(%) when just 16x16 sample points are used. Figure 13 displays the eigenvalue of the plates which are supported as all of edges are simple support with a/b = 1.8 with the roots of shifted Chebyshev and Legendre points. It can be seen that the numerical results agree with the data from theory to within 0.30(%) when just 12x12 sample points are used. It can be observed from Fig. 2-13 that the results solved using the roots of shifted Chebyshev and Legendre points are more accurate than the results solved using the uniform equidistant distribution of discrete grid points and the results solved using 10x10 grid points did not agree with the reference data.
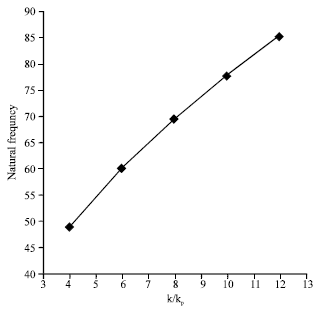 | |
| Fig. 15: | The natural frequencies of the plates that are a spring-mass system mounted on, free at all of edges, except simple supported with torsion spring at half of edge with different k/kp |
Figure 14 shows the natural frequencies of the plates with a spring-mass system and simple supported at all of edge. The data used in this analysis are as follows: a = 1.0 m, b = 1.0 m, h = 0.005 m, v = 0.3, ρh = 39.25 kg m-2, E = 2.051x1011N m-2,D = Eh3/[12(1-v2)] = 2.3478x103 Nxm, MP = ρhab = 2355 kg, kP = D/a2 = 5.8695x102 N m-1 and k/kp = 0.2. The eigenvalue of the spring-mass system mounted on the plate is calculated and this plate is simple supported. The results reveal that ω decrease as M/MP increase. The difference between ω solved using the DQM and ω from reference paper is less than 0.44%.
Figure 15 plots the natural frequencies of the plates that are a spring-mass system mounted on with free at all of edges, except simple supported with torsion spring at half of edge. There is a sprung mass in the central point of the plate. The data used in this analysis are as follows: 15x15 sample points, δx = 10-5, δy = 10-5, a = 1.0 m, b = 1.0 m, h = 0.005 m, v = 0.3, ρh = 39.25 kg m-2, E = 2.051x1011N m-2, D = Eh3/[12(1-v2)] = 2.3478x103 NHm, MP = ρhab = 2355 kg, kp = D/a2 = 5.8695x102 N/m, kφa/D and M/Mp = 0.1. It is worthy of mentioning that Mp is the total mass of plate and kp is the stiffness of the plate. The results indicate that the magnitude of ω increases as k/kp increases.
CONCLUSIONS
The differential quadrature method is shown a powerful means of obtaining accurate solutions to the problem of rectangular plates with various boundary conditions and sprung masses. The natural frequencies of the plates increase as the torsion spring stiffness increases. The natural frequencies of the plates with sprung mass decrease as the weights of the sprung masses increase. The investigation into the integrity of the various grid spacing schemes indicates that the use of unequally spaced grids in conjunction with the technique can produce the fastest convergence. The comparisons and numerical examples show the effectiveness of the differential quadrature method.
REFERENCES
- Gorman, D.J., 1997. Accurate free vibration analysis of shear-deformable plates with torsion elastic edge support. J. Sound Vib., 203: 209-218.
CrossRef - Grossi, R.O. and L.G. Nallim, 1997. A note on the strain energy stored in rotational springs at the plate edges of non-uniform thickness. J. Sound Vib., 206: 448-452.
Direct Link - Laura, P.A.A. and R.O. Grossi, 1981. Transverse vibrations of rectangular plates with edges elastically restrained against translation and rotation. J. Sound Vib., 75: 101-107.
CrossRef - Xiang, Y., K.M. Liew and S. Kitipornchai, 1997. Vibration analysis of rectangular mindlin plates resting on elastic edge supports. J. Sound Vib., 204: 1-16.
CrossRef








