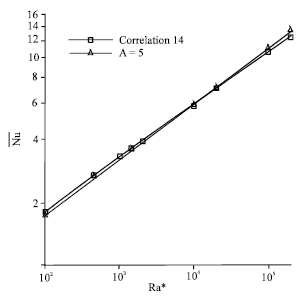
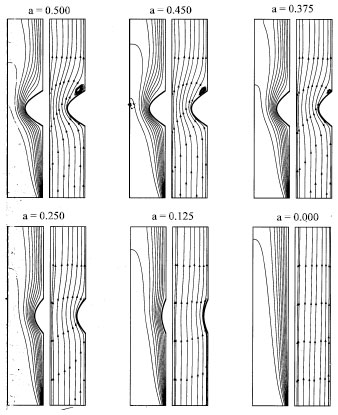
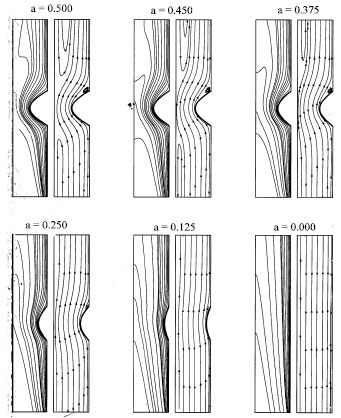
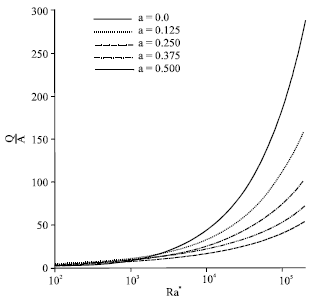
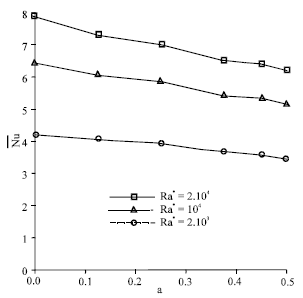
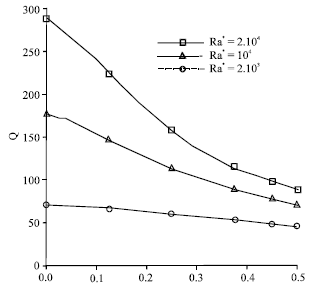
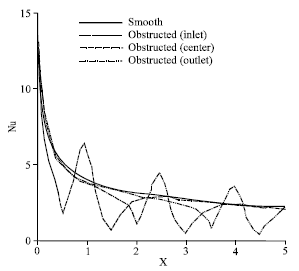
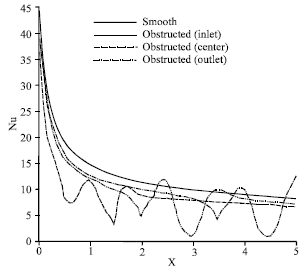
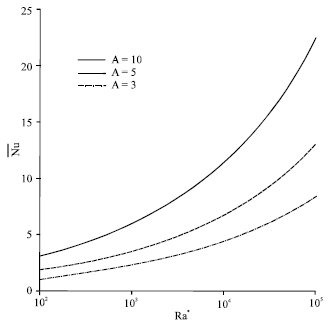
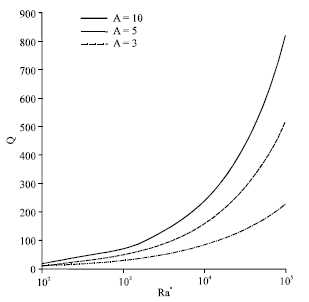
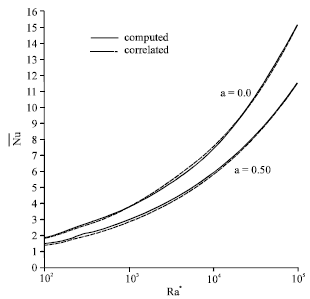
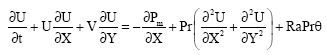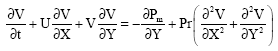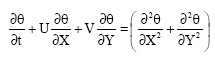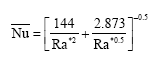Research Article
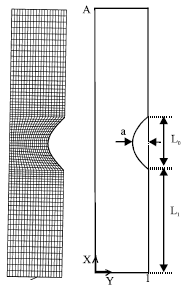
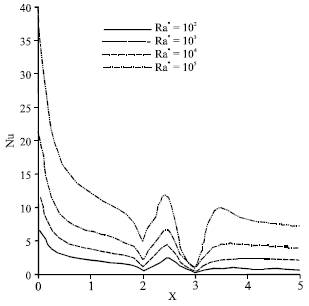
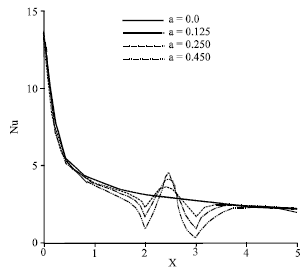
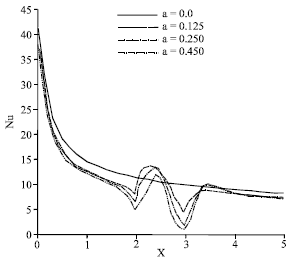
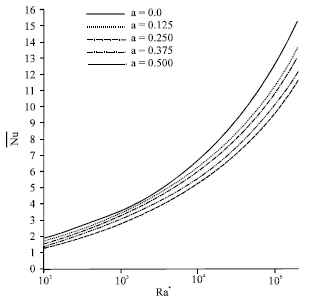
Laminar Natural Convection in a Vertical Channel with a Sinusoidal Obstruction
Institute of Mechanical Engineering, C.U.Bechar, Bechar. Algeria
Rebhi Mebrouk
Institute of Mechanical Engineering, C.U.Bechar, Bechar. Algeria
Draoui Belkacem
Institute of Mechanical Engineering, C.U.Bechar, Bechar. Algeria
Chikh Salah
Faculty of Mechanical and Process Engineering, USTHB, Algiers, Algeria