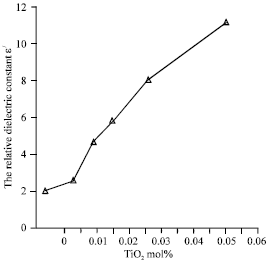
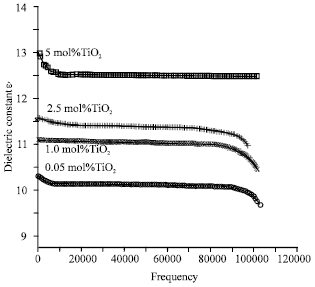
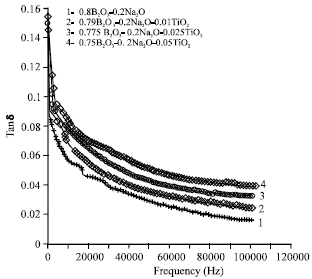
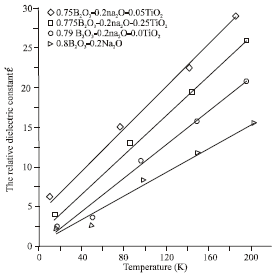
Research Article
Optical and Electrical Properties of Borate Glasses in the System: B2O3/Na2O/TiO2
Faculty of Science, Department of Physics, Al Azaher University, Assuit Branch, Assiut, Egypt
El Sayed Mostafa
Faculty of Science, Department of Physics, Al Azaher University, Assuit Branch, Assiut, Egypt
Amin El-Adawy
Department of Physics, Faculty of Science, Monofia University, Shebin Elkom, Monofia, Egypt