Research Article
Determination of Hydro-chemical Parameters of Salt Transportation in Soil by Using the Solution of Convective Diffusion Equation
Department of Soil Science: Faculty of Agriculture, Ondokuz May1S University, 55139 Samsun, Turkey
Different mathematical models are used for expression of transportation processes in soil. The empiric (static, observation) models, which are used very often among these models, are derived based on statistical evaluation of results obtained from many observations. Such models consider fundamental factors effecting soil processes in general, not in detail. Generally, the models of such kind make applications that are outside of the experimental conditions very hard by not taking mechanisms of soil processes and cause-result relationship into account (Aydarov, 1985).
Theoretically, it is possible to express the mathematical expression of all factors in researches and processes with ideal or complete models (Pollyak, 1976; Yemelyanov et al., 1978; Pachepsky, 1990). These models enable the research of different factors, processes and relationships between them. The determination of parameters included in ideal (or complete) models necessitates implementation of many experimental studies. Rapid variance of some soil properties and consequently, rapid variance of experimental conditions of model parameters based on time and place makes the control and implementation of ideal (or complete) models practically impossible. Therefore, simplification of these models based on scientific facts enables their application in solution of theoretical and practical subjects (van Genuchten et al., 1977; Shukla et al., 2002; Nobuo et al., 2003).
The calculation of water-salt variance in soil, amount of washing water to be used for soil improvement and timing of its implementation, heat transportation, etc. can be conducted by usage of theoretical (half-empiric) models. These models are derived based on universal laws (mass conservation, thermodynamic equations, similarity and criterion theory, etc.) (van Genuchten and Wagenet, 1989; Mikaiylov and Pachepsky, 2003; Gülser and Ekberli, 2004).
Taking homogeneous structure of soil into account, the mathematical expression of processes in soil is achievable by application of theoretical (semi-empiric) models, which necessitate determination of hydro-chemical parameters for different soils depending on soil properties. The factors, such as climate-soil conditions, filtration in soil, evaporation, humidity, etc. effect hydro-chemical parameters significantly. The practical value of application of convective diffusion equation’s solution in water-salt variance of soil and its estimation depends on accuracy of hydro-chemical parameters (Mikaylov and Azizov, 1985; Ekberli and Gülser, 2001). The hydro-chemical parameters comprises many physico-chemical and hydrological factors, which effect water and salt variance in soil, but aren’t widely subject to research. The determination of hydro-chemical parameters in porous media also depends on limit conditions of convective diffusion equation (Aydarov, 1985; Ellsworth et al., 1996). The analytical expressions of diffusion and dispersion processes in soil are also related with hydro-chemical parameters depending on solution of convective diffusion equation (Ellsworth et al., 1996; Shulka et al., 2003). The hydro-chemical parameters have an obvious effect on occurrence of salt transportation in soil as a result of water injection to soil. Depending soil properties, hydro-chemical parameters are determined in laboratory and arable field experiments with different approaches (Lee et al., 2000).
The objective of this research is determination of analytical expressions used in calculation of some hydro-chemical parameters of soils that are comparatively hard to determine in arable field experiments by using the solution of theoretical (semi-empiric) model and calculation of some hydro-chemical parameters’ values.
The application of scientific-technical methods in harmony is essential for the most optimum exploitation of soil fertility. Nowadays, the application of different mathematical models in agriculture is increasing, like in all other areas. The soil improvement depends on realization of soil improvement methods as a result of determination of salt transportation in soil. The quantitative evaluation of salt transportation in soil and its estimation is possible by usage of theoretical (semi-empiric) convective diffusion equation’s solution, which is based on the equation’s valid beginning and limit conditions, as well.
The adequacy of derived mathematical model to the values obtained from arable field experiments is highly related with determination of hydro-chemical parameters and their accuracy. The mathematical models for calculation of hydro-chemical parameters based on solution of convective diffusion equation were determined by taking the results of arable field experiment, which are determined easily, into account. In calculation of hydrochemical parameters, the data obtained as a result of research conducted in the saline-sodic soils of the Lower Kızılırmak Plain in Turkey by Sönmez (1990) are used.
RESULTS AND DISCUSSION
In the process of determination of salt regime in soil and usage of mathematical models, approximately 20 numeric parameters in soil-underground water system are needed to be determined. Although, parameters, such as filtration coefficient, porosity level, etc. can be easily determined, the determination of parameters, such as convective diffusion coefficient, soil transportation in soil, soil dissolvement coefficient, is very hard and necessitates conduction of special studies (Anonymous, 1976).
The below equation represents transmission of water, which is poured on soil surface for washing purposes, to lower layers or to drainage and salt dissolvement by that water (Verigin et al., 1979; Mikaiylov, 1997; Mikayilov and Ekberov, 1999; Mikaiylov and Pachepsky, 2003)
| (1) |
In this equation D = Dm + λυ,-convective diffusion coefficient; Dm-molecular diffusion coefficient; λ-hydrodynamic dispersion coefficient that expresses internal structure of filtration environment; υ (t)-filtration speed; γ-dissolvement speed coefficient; Cd- concentration of solution; C(x,t)-soil concentration on x point of soil during t time. As the washing time is considered as, ![]() , Dm≈0 is considered (Verigin et al., 1979).
, Dm≈0 is considered (Verigin et al., 1979).
The numerical and analytical solution of Eq. 1 obtained in different limit and beginning conditions (Brenner, 1962; Polubarinova-Kocina, 1977; Averyanov, 1978; Mikayılov, 1979; Akperov, 1989; Mikaiylov and Pachepsky, 2003), are used for determination of water-salt regime estimation and hydro-chemical parameters.
In case average integral value of salt amount is ![]() and initial salt dispersion is constant (C0(x) = C0 = constant in R layer of soil, total soil concentration in R layer of soil after washing is expressed as following (Mikaylov and Azizov,1985; Mikayilov and Ekberov, 1999; Ekberli and Gülser, 2001):
and initial salt dispersion is constant (C0(x) = C0 = constant in R layer of soil, total soil concentration in R layer of soil after washing is expressed as following (Mikaylov and Azizov,1985; Mikayilov and Ekberov, 1999; Ekberli and Gülser, 2001):
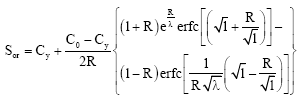 | (2) |
In this equation, Cy-soil concentration of water used for washing; l= τ/m (τ-amount of water used for washing; m-the level of porosity); erfc-known Gauss error (integral) function (Likov, 1967). The expression (2) is obtained as a result of considering equal dispersion of initial saltiness along soil profile during washing period (Aydarov et al., 1982).
| (3) |
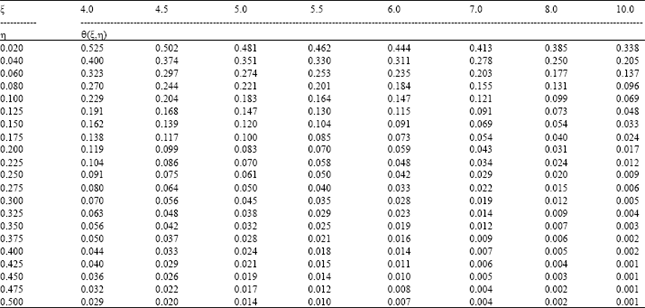
| Table1: | Values of θ(ξ,η) function |
 | |
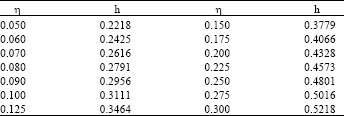
| Table 2: | The values justifying η ctg h = h equation for special values of η |
 | |
Eq. 2 can be expressed in more simplified way:
 | (4) |
The variance of salt concentration in R layer of soil is calculated based on expression (4) by giving values to ξ and η parameters. The obtained results are shown in Table 1. The calculation of hydro-chemical dispersion coefficient is possible, if amount of salt and washing water after washing in soil layer is determined based on Table 1 and values of m, R, Cy, C0, Sor and τ are known.
In the research conducted for improvement of salty-sodium soils of area called as Lower Kızılırmak Plain in Turkey (Sönmez, 1990), for R = 100 cm soil layer, m = 0.49; Cy = 1.5 mmhos/cm; C0 = 19.26 mmhos/cm; Sor = 3.43 mmhos/cm; τ = 270 cm data are obtained.
According to these data and expression (3), the values of θ and ξ are calculated (θ≈0.109, ξ≈5.5). Based on θ and ξ values, η = 0.015 is found by referring to Table 1. The hydro-chemical dispersion parameter will be λ = lm/4x0.150 = 1.667 m by referring to the expression of λ = R/4η .
The Peklet coefficient (Pe), which is considered to have no criterion and is included in solution of water-salt transportation models (Likov,1967; Averyanov, 1978; Mikaylov and Azizov, 1985) , will be calculated as
Pe = 0.6 from the expression of
After determination of λ, m, R, τ, Cy, C0 parameters,
are calculated, θ(ξ*, η*) = θ* is found by referring to Table 1 and salt concentration in soil layer is determined based on the expression of Sor = Cy+(C0-Cy)θ*.
In order to reach salt concentration amount (Sivor) that is acceptable to remain in R layer of soil, parameters of λ, m, R, Cy, C0 Sivor have to be known for the calculation of needed water amount -Ny. Taking these values into account θ* = ![]() - Cy/C0 - Cy and η* = R/4λ are calculated and ξ* = τ/mR is found by referring to Table 1. Based on obtained values, the amount of washing water is determined as Ny = mRξ*.
- Cy/C0 - Cy and η* = R/4λ are calculated and ξ* = τ/mR is found by referring to Table 1. Based on obtained values, the amount of washing water is determined as Ny = mRξ*.
Volobuyev Equation obtained from many number of field experiments is as following:
(α-the level of salt amount that is possible to wash away parameter, which is related to soil structure and soil composition) (FAO/UNESCO, 1973). Theoretically, this expression is obtained from convective diffusion equation as following (Verigin et al.,1986):
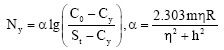 | (5) |
In this equation h, ηctg h = h are values justifying transandent equations, whose some special values are shown in Table 2. If the values of m, λ, Cy, C0, RveSt are known, the amount of washing water can be calculated from expression (5), also the α parameter can be found by determining h value complying to η from Table 2.
Based on the calculated η = 0.15 value, h = 0.3779 is found from Table 2. By taking the above values into account; α = [2.303 x 0.49 x 0.15 x 1]/[(0.15)2 + (0.3779)2] ≈ 1.024 is obtained.
The expression (4) enables determination of soil amount in certain layer of soil, calculation of the amount of washing water and λ-hydro-chemical, Pe-Peklet parameters, which are important in modeling of salt regime, based on amount of salt in layer of soil before and after washing process.
The Table 1, which consists of values obtained from the function θ(ξ,η) by using computer, makes the calculation of λ parameter, Ny-amount of water to be used for washing and the soil concentration amount in soil layer that will be washed easier.
The calculation of α-the level of salt amount that is possible to wash away, which is generally related to soil structure and salt composition parameters, can be realized by using the Eq. 5.