Research Article
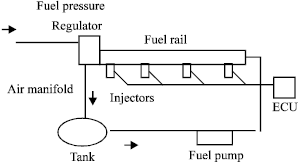
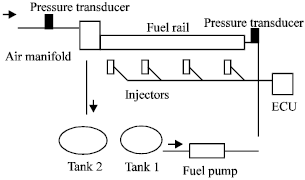
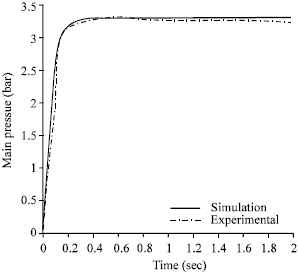
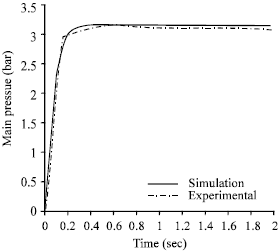
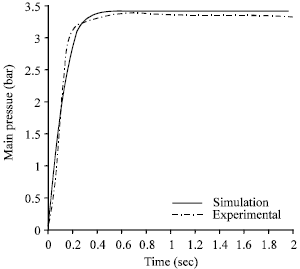
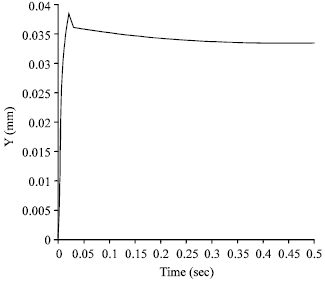
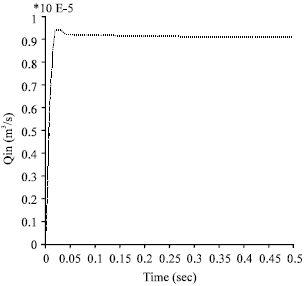
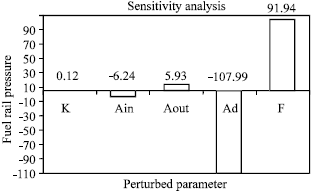
Simulation, Testing and Sensitivity Analysis of Fuel Pressure Regulator for MPFI Paykan 1600 cc Engine
Department of Power and Machinay, University of Tehran, Iran
A. Keyhani
Department of Power and Machinay, University of Tehran, Iran
M. Rahimi
Department of Power and Machinay, University of Tehran, Iran