ABSTRACT
In this study, Gene Expression Programming (GEP) is used to model evaporation using the meteorological data recorded from Automated GroWeather meteorological station near Lake Egirdir. Daily meteorological variables used in modeling are air temperature, solar radiation and relative humidity. Penman method daily evaporation estimations are used as output data for the verification of GEP approach. It is observed that GEP model is capable of yielding good model alternative with a high coefficient of determination and low mean square error as 0.95 and 0.125, respectively. It can be suggested that GEP approach is an alternative model of Penman method.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.508.512
URL: https://scialert.net/abstract/?doi=jas.2005.508.512
INTRODUCTION
Although there is always continuous exchange of water molecules to and from the atmosphere, the hydrologic definition of evaporation is limited to the net transfer of vapor to the atmosphere. This change in state requires an exchange of approximately 600 cal for each gram of water evaporation. If the temperature of the surface is to be maintained, these large quantities of heat must be supplied by radiation and conduction from the overlying air or at the expense of energy stored below the surface[1].
Estimation of evaporation is important for water planning, management and hydrological practices. There are many methods available for estimating potential evaporation from a water surface, comprising both direct and indirect methods. The direct methods include U.S. Weather Bureau Class A pan measurements. The indirect methods, in increasing order of complexity and data requirements, include temperature based formulae (e.g. Blaney-Criddle method), temperature and radiation based formulae (e.g. Priestley-Taylor method), combination formulae which include allowance for humidity and wind (e.g. Penman or Penman-Monteith method), or even more intensive evaluations of energy balance at the evaporating surface[2]. These and similar methods are used and compared for evaporation estimation by many researchers[2-8]. Although these approaches are based directly on the Penman method, they are rather restrictive and sensitive to side specific evaporation estimations, which can vary widely from one lake to another. It is not possible to consider all the evaporation affecting factors simultaneously by none of the aforementioned single approaches over a time span. On the other hand, there are many restructured phenomenological and procedural restrictive assumptions which limit the applicability of any methodology except under specific circumstances and conditions.
GEP is a genotype/phenotype system that evolves computer programs of different sizes and shapes (expression trees) encoded in linear chromosomes of fixed length. The genetic encoding used in GEP allows a totally unconstrained interplay between chromosomes and expression trees. This interplay brought about a tremendous increase in performance allowing, consequently, the undertaking of detailed, much needed analysis of fundamental evolutionary processes[9].
In this study an alternative method is proposed for evaporation estimation from water surface by using Gene Expression Programming (GEP). This method relates various factors that affect evaporation rate and in the modeling actual measurements are employed. In the application part of the study, evaporation estimations from Penman methodology are used for modeling by GEP, which is capable to mimic, measured and estimated evaporation data for the best evaporation estimations. GEP training catches the underlying generation mechanism of evaporation phenomenon and then provides estimations given the input variables only. Hence, the model is first trained by exploiting part of measurements and then the evaporation estimations are given provided that only the input factors are provided. The reason for such an approach is to incorporate in GEP model the possible uncertainties in data measurements and hence to digest the whole measured data collectively within a single model. On the contrary, Penman equation treats the data individually for a particular time period. In fact, GEP treats the whole available data for depicting evaporation phenomenon behavior over longer time periods.
The main purpose of this study was to develop a model by Gene Expression Programming (GEP) for estimating evaporation from meteorological parameters which are comparatively easier for measurements.
Gene expression programming: The fundamental unit of information is in living systems in the gene. In general, a gene is defined as a portion of a chromosome that determines or affects a single character or phenotype (visible property), for example, eye colour. It comprises a segment of deoxyribonucleic acid (DNA), commonly packaged into structures called chromosomes. This genetic information is capable of producing a functional product which is most a protein.
Genetic Algorithm (GA) is inspired by the mechanism of natural selection where stronger individuals are likely the winners in a competing environment. Here, GA uses a direct analogy of such natural evolution. Through the genetic evolution method, an optimal solution can be found and represented by the final winner of the genetic game[10].
The phenotype of GEP individuals consists of the same kind of ramified structures used in genetic programming. However, these complex entities are encoded in simpler, linear structures of fixed length-the chromosomes. Thus, there are two main players in GEP: the chromosomes and the ramified structures or expression trees, the latter being the expression of the genetic information encoded in the former. Figure 1 shows an example of expression trees.
As in nature, the process of information decoding is called translation. And this translation implies obviously a kind of code and a set of rules. The genetic code is very simple, a one-to-one relationship between the symbols of the chromosome and the functions or terminals they represent. The rules are also very simple: they determine the spatial organization of the functions and terminals in the expression trees and the type of interaction between sub-expression trees in multi-genic systems. In GEP there are therefore two languages, the language of the genes and the language of expression trees.
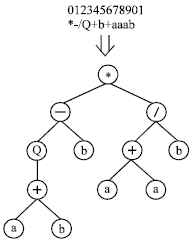 | |
| Fig. 1: | An example of expression trees |
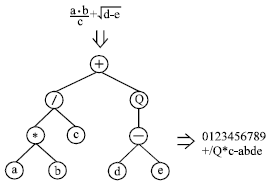 | |
| Fig. 2: | An example of Karva language |
However, thanks to the simple rules that determine the structure of expression trees and their interactions, it is possible to infer immediately the phenotype given the sequence of a gene and vice versa. This bilingual and unequivocal system is called Karva language. Figure 2 shows an example of Karva language[11].
Penman method: In 1948, Penman presented a theory and formulae for the estimation of evaporation from weather data. The theory is based on two requirements, which must be met if continuous evaporation is to occur. These are: (i) there must be a supply of energy to provide latent heat of vaporization; (ii) there must be some mechanism for removing the vapor, once produced. The formula has been checked in many parts of the world and gives good results. Being based on physical principles, it is of general application and gives values that should serve for most project studies until supplemented by actual evaporation measurements. Penman formulae can be given as follow:
| (1) |
where:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
and
| (7) |
in which E: evaporation (mm/day), Δ: slope of vapor pressure versus temperature curve (kPa°C-1), γ: psychometric constant (kPa °C-1), Ta: air temperature (°C), Tw: water temperature (°C), Pa: air pressure (kPa), λ: latent heat of vaporization (°C), u2: wind speed at 2 m height (m s-1), Rn: net radiation (cal/cm2/day), RC: short wave radiation (cal/cm2/day), RB: long wave radiation (cal/cm2/day), RA: Angot’s value of solar radiation (g cal/cm2/day), α: albedo constant = 0.08, σ: Lummer constant = 117.4x10-9 (g cal/cm2/day), n/D: actual/possible hours of sunshine, ew: the saturation vapor pressure of air at temperature Ta (kPa), ea: the actual vapor pressure of air at temperature Ta (kPa)[12].
Study region and data: Lake Eğirdir (latitude 37.80-38.43°N; longitude 30.30-31.37°E) is a freshwater lake located in the Lakes District of Turkey. It is the second largest lake in the country with 47x107 m2 surface area and a volume of 4360x106 m3 (Fig. 3) and is used as a source of drinking and irrigation water. Lake Eğirdir is of tectonic origin and lies on a 50 km stretch in the northern part of Eğirdir Country.
| Table 1: | Structure of the model |
 | |
The altitude of the lake is 916 m above mean sea level. The distance between the east and west shores is 3 km and the mean depth of the lake is 8-9 m with the deepest point at 15 m. In the southern part, the width of the lake reaches a maximum of 16 km.
Meteorological data to develop the GEP model were obtained from the Automated GroWeather Meteorological Station located near Lake Eğirdir. Meteorological parameters included air and water temperature, relative humidity, solar radiation, wind speed, air pressure and sunshine hours. The data used to develop GEP model include daily observations from 2001 and 2002 years.
Application: In this study, the methodology described above was applied to data for year 2001 in order to model evaporation. Data for year 2002 are used to test the model. System inputs include the air temperature (Ta), solar radiation (RC) and relative humidity (Rh). Output is the evaporation estimations from Penman methodology (E). It is showed the structure of the used model in Table 1.
At the end of 15000 generation, best fitness was found as 22026.05. Figure 4 and 5 show the regression curves of training and testing sets of the model, respectively. The model results lie around a 45° straight line implying, that there are no bias effects.
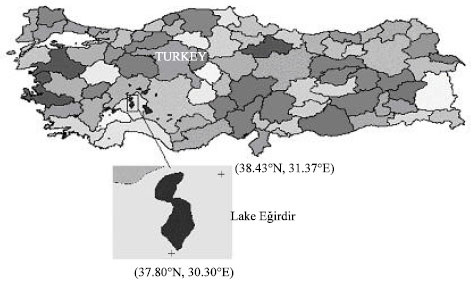 | |
| Fig. 3: | Location of Lake Egirdir, Turkey |
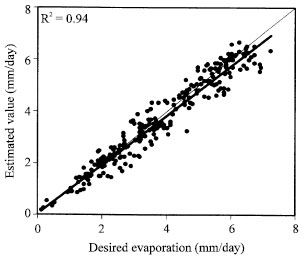 | |
| Fig. 4: | Scatter diagrams between GEP model and Penman method for training set |
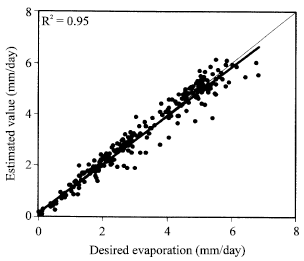 | |
| Fig. 5: | Scatter diagrams between GEP model and Penman method for testing set |
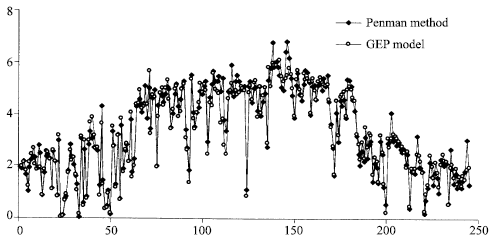 | |
| Fig. 6: | Evaporation values of Penman method and the GEP model for testing set |
The results of the model and Penman method are presented in Fig. 6, where the model matches daily evaporation more closely to Penman method. Coefficients of determination (R2) of training and testing sets of the developed model are obtained as 0.94 and 0.95, respectively. Mean square error (MSE) values are obtained 0.195 and 0.125, respectively.
The evaporation formula obtained from GEP is shown in Eq. 8.
| (8) |
CONCLUSIONS
Evaporation is one of the fundamental elements in the hydrological cycle. Effective and simple evaporation estimations are required in any water related engineering study. Especially, evaporation estimation from readily measurable meteorological factors is the most preferred formulation. Unfortunately, such approaches are rather scarce in the literature. In this study, a model is developed to estimate evaporation as an alternative model of Penman method using GEP approach. Evaluating performance of the developed model, it requires less meteorological parameter than Penman method and has high coefficient of determination. It is concluded that GEP model can be used to estimate daily Penman evaporation.
REFERENCES
- McKenzie, R.S. and A.R. Craig, 2001. Evaluation of river losses from the Orange River using hydraulic modeling. J. Hydrol., 241: 62-69.
CrossRefDirect Link - Choudhury, B.J., 1999. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol., 216: 99-110.
Direct Link - Vallet-Coulom, C., D. Legesse, F. Gasse, Y. Travi and T. Chernet, 2001. Lake evaporation estimates in tropical Africa (Lake Ziway, Ethiopia). J. Hydrol., 245: 1-18.
CrossRef - Keskin, M.E., O. Terzi and D. Taylan, 2004. Fuzzy logic model approaches to daily pan evaporation estimation in western Turkey. Hydrol. Sci. J., 49: 1001-1010.
CrossRefDirect Link - Terzi, O. and M.E. Keskin, 2005. Modeling of daily pan evaporation. J. Applied Sci., 5: 368-372.
CrossRefDirect Link - Chow, T.T., G.Q. Zhang, Z.L. Lin and C.L. Song, 2002. Global optimization of absorption chiller system by genetic algorithm and neural network. Energy Build., 34: 103-109.
Direct Link - Ferreira, C., 2002. Gene Expression Programming in Problem Solving. In: Soft Computing and Industry-recent Applications, Roy, R., S. Ovaska, T. Furuhashi and F. Hoffman (Eds.). Springer-Verlag, Uk, pp: 635-654.
CrossRefDirect Link








