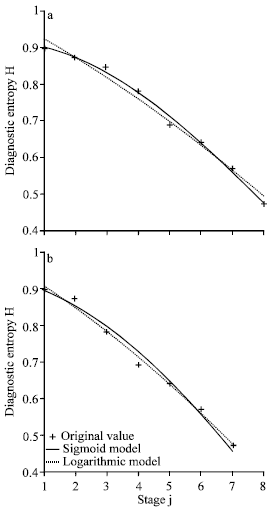
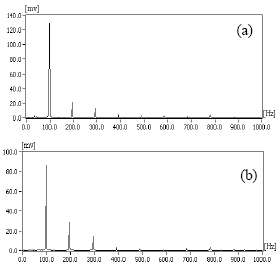
Research Article
Sigmoid Model: A Simulation for Inference Process of Engineering Diagnosis
Research Institute of Diagnostics and Cybernetics, Xian Jiaotong University, Xian, Peoples Republic of China, 710049
Zhaoyong Hu
Research Institute of Diagnostics and Cybernetics, Xian Jiaotong University, Xian, Peoples Republic of China, 710049