ABSTRACT
Fermat`s principle applied to a flat metric in the plane yields the phase of a Bessel function in the periodic domain for a constant index of refraction. Gravitational forces cause the index of refraction to vary and lead to a modified phase of the Bessel function. A distinction is made between the forces that cause acceleration: the gravitational force affects the optical properties of the medium whereas the centrifugal force does not, the latter being built into the phase of oscillations of the Bessel function. The time delay in radar echoes from planets is determined from Fermat`s principle where the velocity of light is the phase velocity and the index of refraction varies on account of the gravitational potential. The deflection of light by a massive body is shown to be produced by a quadruple interaction and the perihelion shift requires both the gravitational potential, producing a closed orbit and the quadruple, causing the perihelion to rotate.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2005.299.308
URL: https://scialert.net/abstract/?doi=jas.2005.299.308
INTRODUCTION
General relativity is based on the notion that gravity, rather than being a force between masses, is the curvature of spacetime. The source of curvature is mass itself, like the source of an electric field is charge. Just as free particles follow straight lines in flat spacetime, free particles follow geodesics in the curved spacetime of a gravitational field. The calculations of the red shift, the time delay in radar echoes from planets, the bending of light, the perihelion shift and the geodesic effect all support general relativity.
Sometimes new insight can be gained in looking at old results from a new perspective. The old quantum theory of multiply-periodic central motion was superseded by wave mechanics. Old quantum theory attempted to apply celestial mechanics to the world of atoms with the addition of quantum restrictions to the motion[1]. This study will apply it to diffraction phenomena in the short-wavelength limit that involve the relativistic effects of time delay in radar sounding, the deflection of light and the advance of the perihelion-three of the so called five tests of general relativity. Moreover, these relativistic effects are static so that they can be investigated by studying only the spatial component of the metric. The trajectory of a light ray in a static gravitational field is determined in the same way as in an inhomogeneous refractive medium[2]. Fermat’s principle of least time relates the length and orientation of a light ray to the time for light to propagate along the ray path. The analogy between the index of refraction and the square root of twice the difference between the total and potential energies is also well known. Yet, this can provide a way of distinguishing between the centrifugal and gravitational fields which cause acceleration and the form of the trajectory of the motion.
If we take a flat space time metric in the plane and consider a constant index of refraction, we will show that Fermat’s principle yields precisely the phase of the oscillations of the Bessel function of the first kind in the periodic domain in the asymptotic, short-wavelength, limit. This is the same as the WKB result, and it allows us to associate a wave phenomenon with a geodesic trajectory. The only potential appearing is the repulsive centrifugal potential and the trajectory is necessarily open. In contrast to general relativity, where gravity is not considered as a force in the conventional sense, but, rather, built into the curvature of spacetime, the centrifugal force is built into the phase of the Bessel function in the periodic domain, where the trajectory consists of straight line segments and arc lengths on a caustic circle whose radius is determined by the magnitude of the angular momentum. Whereas all forces causing acceleration are on the same footing in general relativity, the gravitational force and not centrifugal force, has to be introduced through a space varying index of refraction in an inhomogeneous refractive medium. The effect of gravity is to make the medium optically more dense in the vicinity of a massive body, while the centrifugal force has no effect on the optical properties of the medium. Centrifugal, Coriolis and gravitational forces are usually considered to be fictitious insofar as they can be transformed away by a change of frame. The centrifugal and Coriolis forces can be transformed away by changing to a nonrotating frame, while the fictitious force of gravity is transformed away by changing from a nonfreely falling to a freely falling frame. In Newtonian theory one insists on a nonrotating frame, but not a freely falling one. Here, we appreciate that the force of gravity affects the optical properties of the medium whereas the centrifugal force determines the radius of the caustic circle and the diffraction pattern in its neighborhood.
The time delay in radar sounding, the bending of light in the vicinity of a massive body and the advance of the perihelion will be treated from this view point. The introduction of the Newtonian potential will cause a modification of the phase of the Bessel function and yield both periodic and aperiodic orbits depending upon whether the total energy is negative or positive, respectively. The time delay in radar sounding is a double relativistic effect that is caused by the slowing down of clocks in the vicinity of a massive body, accounted for by the fact that light travels at the phase velocity and the shrinking of measuring rods, accounted for by a line element that is magnified by the index of refraction. Since an index of refraction that takes into account the Newtonian gravitational potential only gives one half the relativistic value it cannot be the cause, or at least the entire cause, of the bending of light. Rather, if we take the next higher interaction into account that causes mass to accelerate we do find the actual general relativistic value without the Newtonian gravitational potential. This implies that, like gravitational radiation, the interaction between a light ray and a massive body is predominantly quadruple.
In contrast, the advance of the perihelion requires both gravitational potential and the quadruple interaction. In general relativity, the quadruple appears as a relativistic correction to the square of the transverse velocity in the conservation of energy. The gravitational potential is responsible for the closed elliptical orbit, while the quadruple causes the perihelion to slowly rotate producing a rosette orbit. A dipole moment would have been sufficient to cause the advance of the perihelion[1], but, since there is conservation of momentum, the center of mass of the system cannot accelerate and so the mass dipole moment cannot accelerate.
METRIC AND PHASE
Fermat’s principle states that the ray path connecting two arbitrary points makes the optical path length stationary
| (1) |
where, η is the index of refraction and T is the kinetic energy per unit mass. As a first application of Fermat’s principle we calculate the time delay in radar sounding. In general relativity, this time delay is predicted by the Schwarzschild metric evaluated on the null geodesic when all angular dependencies are ignored. If a light signal is sent from the earth, located along the x-axis at -xE, to Venus, which is located behind the sun at xV, the light ray will be bent as it passes the gravitational field of the sun. Clocks will be slowed down and the time it takes the ray to bounce off Venus’ surface and return to earth will be longer than if the sun were not present.
The simplest mechanical analog of the index of refraction is ![]() , where, U is the potential energy per unit mass and c is the speed of light in a vacuum. Since the gravitational field of the sun makes the medium optically more dense, U is identified as the gravitational potential -GM/r, where, G is the Newtonian gravitational constant, M is the sun’s mass,
, where, U is the potential energy per unit mass and c is the speed of light in a vacuum. Since the gravitational field of the sun makes the medium optically more dense, U is identified as the gravitational potential -GM/r, where, G is the Newtonian gravitational constant, M is the sun’s mass, ![]() is the distance from the center of the sun to Venus and R is the radius of the sun.
is the distance from the center of the sun to Venus and R is the radius of the sun.
Now, according to Fermat’s principle, the propagation time t along a ray connecting the two endpoints - xE and xV is given by:
where, R: = 2GM/c2 is the Schwarzschild radius. The slowing down of clocks in a gravitational field will result in an apparent reduction in the speed of light.
Light will therefore travel at the phase velocity u(r) = c/η(r), rather than c, as it would in vacuum. Consequently, the travel time will be:
where, tN = (xV + xE)/c is the Newtonian travel time. The second term is half the time delay for a signal to bounce off Venus and return to the earth. Fermat’s principle thus predicts a time dilatation of
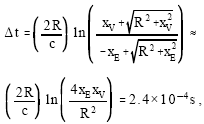 |
where, the square roots have been expanded to lowest order using the fact that R ‹‹ xV, xE.
This simple application of Fermat’s principle gives the same result as general relativity. In a simplified demonstration of the time delay of radar sounding caused by a massive body[4], t =∫ dx/ceff, where, ceff = (1-R/2r)2 c≈ (1-R/r)c, is an ‘effective speed’ that supposedly accounts for both time dilatation and the shrinking of measuring rods in a gravitational field. The final expression for t is valid to first order in R/r. Rather, in our presentation, the expression for t is exact and it is a result of two factors: the slowing down of clocks, as expressed by the fact that light rays propagate at the phase velocity, c/η(r) and the warping of measuring sticks, as accounted for by the stretching of the line element, η(r)dx. If the effective velocity ceff were to be identified as the phase velocity, then this would account for only half of the effect and which is to within 3 % of experimental uncertainty[3]. In the following, we will use gravitational units where c = G = 1 and the more general expression for the index of refraction:
| (2) |
where, the dimensionless constant-A represents the negative of twice the total energy, allowing for both positive and negative values.
In a rotating coordinate system in the Euclidean plane (θ = π/2):
| (3) |
Fermat’s principle will determine the phase of the wave function ψ that is a solution of Helmholtz’s equation:
(Δ+κ2) ψ = 0, |
in the short-wavelength, or high-wave number κ, limit, where Δ stands for the Laplacian. The solution to Helmholtz’s equation can be written as
| (4) |
where, A is a constant term in the amplitude, ![]() are phases of the incoming and outgoing waves, and
are phases of the incoming and outgoing waves, and ![]() is an integration constant that will be determined by matching conditions between the periodic and exponential domains [vid. (15) below]. The prime denotes differentiation with respect to r. The function S is referred to as the eikonal and it is the object of our study.
is an integration constant that will be determined by matching conditions between the periodic and exponential domains [vid. (15) below]. The prime denotes differentiation with respect to r. The function S is referred to as the eikonal and it is the object of our study.
Introducing (3) into (1) implies that the ray path connecting two arbitrary points makes the optical length
| (5) |
stationary. Observing that φ is a cyclic coordinate and calling Λ the integrand of (5), we immediately obtain a first integral of the motion
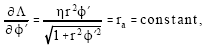 |
regardless of whether the medium is homogeneous or not. In an inhomogeneous medium η will be a function r. For the moment we shall assume that it is a constant. Solving for φ’, we obtain the equation of the orbit as:
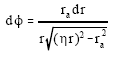 | (6) |
Integration of (6) gives the trajectory:
| (7) |
where, φ0 is a constant of integration. Squaring both sides of (6) and using (2) give the conservation of energy
provided the radius of the caustic[5] is given by:
| (8) |
This is Kepler’s law of equal areas in equal times, or the conservation of angular momentum, where, ![]() is the angular momentum (relative to unit mass). Introducing (6) into (5) results in:
is the angular momentum (relative to unit mass). Introducing (6) into (5) results in:
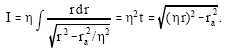 | (9) |
The eikonal is the integral over r of the Legendre transform of the integrand of Fermat’s principle:
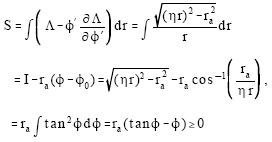 | (10) |
The second line of (10) expresses the eikonal as the difference between (9) and the arc length along the caustic[5]. The third line of (10) shows that the product of ra and (10) is the area of a circular cap whose base is a circular arc of radius ra and whose peak is a distance r from the center of the circle[6]. In other words, the addition of a circular cap to a body increases its area by raS(r), while its perimeter is increased by 2S(r), which is strictly increasing and strictly convex on ra≤r<∞.
The second line of (10) is Debye’s asymptotic expression for the phase of the Bessel function in the periodic region r>ra[7]. In a homogeneous refractive body of a constant index of refraction, a light source is situated a distance r from the center of a circle of radius ra, which is the caustic. The eikonal (10) consists of two rays: a half-line ![]() from the source to the point of tangency to the circumference of a circle of radius r = ra and a ray along the arc length, ra cos-1 (ra/r). This quantity is subtracted from the straight line segment because the ray is taken from the caustic to the source. For the reverse path, the signs of the two terms are exchanged. Apart from a term -¼π, expression (10), when multiplied by k, represents the phase going away from the caustic, while the ray going toward the caustic has the signs reversed in addition to a phase factor of +¼π. Hence, the phase changes abruptly by an amount -½π upon passing through the caustic. A phase jump of this magnitude is observed for a focal line due to the convergence of rays of a cylindrical wave[8].
from the source to the point of tangency to the circumference of a circle of radius r = ra and a ray along the arc length, ra cos-1 (ra/r). This quantity is subtracted from the straight line segment because the ray is taken from the caustic to the source. For the reverse path, the signs of the two terms are exchanged. Apart from a term -¼π, expression (10), when multiplied by k, represents the phase going away from the caustic, while the ray going toward the caustic has the signs reversed in addition to a phase factor of +¼π. Hence, the phase changes abruptly by an amount -½π upon passing through the caustic. A phase jump of this magnitude is observed for a focal line due to the convergence of rays of a cylindrical wave[8].
In the shadow region r<ra, where the rays do not penetrate, the eikonal (10) becomes completely imaginary:
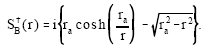 | (11) |
Since the ‘shadow’ intensities vanish rapidly as k, or the distance from the caustic increases, they are usually ignored[9]. However, the matching conditions between the periodic and exponential regions are of fundamental importance in quantum mechanics because they furnish the quantum conditions[10]. Hence we must give credence to the type of motion that occurs in the shadow zone. Interestingly enough, contradictions will arise with the laws of physics that govern the illuminated, or periodic, zone.
For instance, by reinstating the velocity of light c, we have the inequality ![]() in the shadow zone. This is in contradiction with special relativity. However, in the spectrum of a medium of anomalous dispersion there can exist a region near the absorption line where the group velocity can be greater than c[11]. In this region, the group velocity no longer represents the velocity of the signal. Anomalous dispersion that results from strong absorption destroys the characteristic wavelength of propagation so that light can only be defined statistically. For electrodynamic guided waves[11] and in quantum mechanics, the phase velocity is greater than c. The concept of a phase velocity in quantum mechanics was discarded when Schrodinger[12] proved that the group velocity of the wave represented the particle velocity of the electrons. But this meant that individual waves could not be used for signal transmission. Even if they could be, there would still be a detection problem since no optical effect could propagate with a velocity greater than c.
in the shadow zone. This is in contradiction with special relativity. However, in the spectrum of a medium of anomalous dispersion there can exist a region near the absorption line where the group velocity can be greater than c[11]. In this region, the group velocity no longer represents the velocity of the signal. Anomalous dispersion that results from strong absorption destroys the characteristic wavelength of propagation so that light can only be defined statistically. For electrodynamic guided waves[11] and in quantum mechanics, the phase velocity is greater than c. The concept of a phase velocity in quantum mechanics was discarded when Schrodinger[12] proved that the group velocity of the wave represented the particle velocity of the electrons. But this meant that individual waves could not be used for signal transmission. Even if they could be, there would still be a detection problem since no optical effect could propagate with a velocity greater than c.
Boundary conditions in general relativity are usually stated by requiring spacetime to be asymptotically flat, as in the case of the Schwarzschild metric. But, in rotating systems a cutoff must be introduced for otherwise distances ![]() would make the time component of the metric tensor negative[13]. Such a restriction would limit the phase of the Bessel function to the periodic region, but it would not be in the form of an asymptotic boundary condition. Larger distances where the angular velocity becomes greater than the velocity of light would bring us within the caustic region and does not lead to the conclusion that such a system cannot be made up of real bodies[13].
would make the time component of the metric tensor negative[13]. Such a restriction would limit the phase of the Bessel function to the periodic region, but it would not be in the form of an asymptotic boundary condition. Larger distances where the angular velocity becomes greater than the velocity of light would bring us within the caustic region and does not lead to the conclusion that such a system cannot be made up of real bodies[13].
The eikonal (11) can also be derived from Fermat’s principle, which now reads:
| (12) |
Following the same procedure as before, we find the trajectory
| (13) |
for a constant index of refraction, where we can always arrange for φ0 = 0 by suitably fixing the initial point for the measurement of the arc length. The extremum (12) is just the distance ![]()
Using the canonical parameterization for which ra = 1, the arc length s = sinh φ enables the profile curve to be written as:
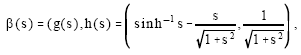 |
where, g(s) measures the distance along the axis of revolution and h(s) measures the distance from the axis of revolution. The parameterization of the surface of revolution is:
 |
where, θ is the angle through which the profile curve has been rotated. The element of arc length on the surface of revolution is:
The eikonal (11) is just the distance along the φ axis,
which in terms of φ,
| (14) |
is a tractrix, having a constant negative curvature, K = -1/r2a. The tangent to the tractrix which intersects the x-axis always has the constant value ra. The distance from the origin to the point of tangency is raφ. The point on the tractrix which has a tangent intercepting the x-axis is located a distance ra (φ-tanh φ) along the x-axis. This is precisely the eikonal (14). Hence, in the periodic domain the eikonal is half the increase in the perimeter due to the addition of a spherical cap to a body, while in the exponential domain, the eikonal is a tractrix, which is the involute of a catenary unwinding from its lowest point.
The solutions to Helmholtz’s equation are now exponentials:
The general solution has two free constants, B+ and B¯, associated with the ± signs in the exponent. The exponential growing solution is unphysical and consequently, it must vanish. The matching condition between the constants A and ![]() in (4) and B+ is[10]:
in (4) and B+ is[10]:
and if it is to vanish,
| (15) |
where, k is an arbitrary integer. This gives rise to the phase jump ei¼π as the system passes through the caustic.
THE MECHANICS OF DIFFRACTION PHENOMENA
Formulas (8) and (9) are familiar from Kepler’s theory, but depend on the form of the index of refraction. In a repulsive field U is positive, or in no field at all, the realness of the index of refraction (2) requires A<0 so that the trajectory is open, extending between r = ∞ and a minimum value of r, where the velocity vanishes.
In an attractive field of force, A can be of either sign. The unperturbed motion will be the result of some playoff between the gravitational potential, U = R/2r and the centrifugal potential, r2a/2r2. Introducing the former into the expression for the index of refraction (2), the eikonal (10) becomes:
 | (16) |
where, the eccentricity
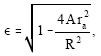 | (17) |
the semi-latus rectum
| (18) |
and a = R/2|A|, which is the semi-major axis if ∈<1. The equation for the orbit is:
| (19) |
which is an ellipse for ∈<1 (A>0), or a hyperbola for ∈>1 (A<0). In the periodic case, φ is known as the ‘true anomaly’ and u is the ‘eccentric anomaly’. The latter satisfies the equation:
in the periodic case, A>0, while it satisfies
in the hyperbolic case A<0.
The velocity
| (20) |
will vanish at
| (21) |
r undergoes a libration, where, the turning points are the aphelion (r+) and the perihelion (r-). In the hyperbolic case, there will be only one point where the velocity (20) vanishes and that is at the closest distance of approach:
| (22) |
A Hankel function of type j, with argument k∈r and order k(q-r) has the integral representation:
| (23) |
The contours Cj are the paths from -π+i∞ to -i∞ and -i∞ to π+i∞. We seek an asymptotic expansion of (23) as k→∞. On the basis of the definitions of the contours Cj, the only critical points of:
| (24) |
are simple saddle points. The necessary condition for simple saddle points, W’(φ±) = 0, gives equation (19), where, φ+ = -φ– with 0<φ+<π and -π<φ─<0. These saddle points will be simple because W"(φ±) = -∈r sin φ± ≠ 0. Evaluating (24) at the saddle points leads to
| (25) |
As ∈64, implying that A<0 and the path is an hyperbola, (25) becomes proportional to the free eikonal (10). The derivative of (25) with respect to r is proportional to the velocity (20) in this limit. We will have need of this limit in the next section when dealing with the bending of light by a massive body.
If q-r>∈r, the order of the Hankel function (23) is greater than its argument. The saddle points φ± now lie on the imaginary axis:
and the phase becomes completely imaginary
This corresponds to the shadow region where the rays do not penetrate. Since the contributions from φ = φ- are exponentially smaller than those from φ = φ+, the former can be neglected; hence, to leading order
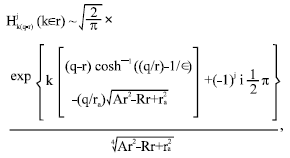 |
for j = 1, 2. The change of signs under the square root sign imply that the gravitational potential is now repulsive, while the centrifugal potential is attractive. In the periodic case, the shadow region lies beyond the limits of libration (21), whereas in the aperiodic case, it is a circle whose radius is smaller than (22). Mechanically, these regions are classically inaccessible while optically, they can be penetrated, like quantum mechanical tunneling and the breakdown of structural stability in catastrophe theory. Near a caustic of the free phase Bessel function, it would be approximated by a cubic resulting in an Airy function. The catastrophe is known as a fold catastrophe[9].
Finally, in the case A = 0, corresponding to a parabolic orbit (∈ = 1), the eikonal is:
 | (26) |
where, ![]() The eikonal (26) is similar to the unbounded, periodic motion of (10), with the exception that the caustic radius ra is magnified by a factor ra/R.
The eikonal (26) is similar to the unbounded, periodic motion of (10), with the exception that the caustic radius ra is magnified by a factor ra/R.
DEFLECTION OF LIGHT
If U is the gravitational potential, the interaction is attractive and the orbit curves towards the center of force. Gravity makes the medium optically more dense in the vicinity of the sun than far away from it. As a result, light waves will be bent around the sun rather than being straight. The effect was originally predicted by Söldner in 1801 and rederived by Einstein in 1911 on the basis of the Doppler effect and Newtonian theory. Specifically, Einstein considered the slowing down of light in a gravitational field[14]. General relativity predicts a value twice as great, as Einstein showed in 1915[14]. It is therefore concluded that Newtonian theory is only an approximation, valid at speeds small compared to that of light and the full theory must be used to calculate the actual deflection of a light beam traveling through the sun’s gravitational field. The value obtained from Newtonian theory is only half that predicted from general relativity. If instead the interaction were quadrupole in nature, the phase of the Bessel function would belong to the periodic domain and thus correspond to a diffraction phenomenon.
The directions of the asymptotes of the hyperbola (19) are determined from the condition r = ∞ which gives:
| (27) |
Since only the rest energy is involved, A = -1 and ∈ = 2ra/R for ra ››R, the total de ection will be twice (27) or:
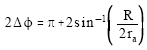 |
A straight ray corresponds to 2Δφ = π. This is comparable to Coulomb scattering, except that the trajectory is concave toward the origin where the massive body is located. For small angles of de ection the angle between the two asymptotes differs from π by θ = R/ra, which is the Newtonian result, but differs from the actual gravitational value by a factor of two. This is used to highlight the shortcomings of Newtonian theory and the need of general relativity[15].
Møller[15] splits the deflection of light into two effects: a velocity of light that varies as ![]() and the non-Euclidean character of the spatial geometry. The first effect gives the radial velocity
and the non-Euclidean character of the spatial geometry. The first effect gives the radial velocity
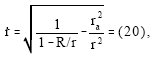 | (28) |
to first order in R/r, while the second effect has a radial velocity:
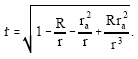 | (29) |
Both give a contribution that is half the general relativistic value. Equation (29), which arises from the Schwarzschild exterior metric tensor, has the wrong sign of gravitational field. It appears repulsive like that of the centrifugal potential. Rather, we shall now show that the de ection of light by a massive body is accountable by the last term in (29), which is a quadrupole interaction, without the incorrect gravitational potential.
When the light ray enters the scattering potential, it enters a region of changing index of refraction, where it is both refracted and diffracted. This is determined by the phase of the wave function. Since the gravitational potential is not responsible for the bending of light, we have to look to a higher order interaction. Expanding the gravitational energy of the central field of force in inverse powers of r we have:
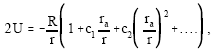 | (30) |
where, the ci are coupling constants and ra is the characteristic length. This is analogous to the Coulomb case, where ra would represent the radius of the first Bohr orbit[16]. The next lowest interaction, c1, would be a mass dipole which, however, cannot oscillate so that its center of mass cannot accelerate. Hence, we set c1 = 0 and consider the quadrupole term, Q/r3, where, Q = Mra is the quadrupole moment of a system consisting of the sun and a photon in the direction perpendicular to the asymptote of the photon trajectory and the parallel line passing through the center of the sun. We shall consider the coupling constant c2 to be of order unity.
It proves convenient[15] to introduce the new variable ![]() into the equation of the trajectory,
into the equation of the trajectory,
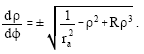 | (31) |
Neglecting the small term Rρ3, the equation of the orbit is (7), which is equivalent to:
where, S is the eikonal of the Bessel function, (10). For a constant index of refraction, the trajectory r = ra/η sin φ, obtained by setting φ0 = ½π, is a straight line which passes through the origin at a distance ra/η when φ =½π and goes to infinity again for φ→π.
The exact equation (31) may be written as[15]:
| (32) |
where, ![]() Since Rρ is a small quantity, we obtain the approximations
Since Rρ is a small quantity, we obtain the approximations
to first order and consequently, radρ = (1+Rσ/ra)dσ. Introducing these approximations into (32) and integrating from 0 to the distance of closest approach, θ0, we get:
| (33) |
In the derivation of (33) we have used the fact that the distance of closest approach is determined by the vanishing of the integrand in the denominator and hence, σ0 = 1. Consequently, the deflection θ = 2 R/ra is twice that obtained by treating the interaction through a Newtonian potential. The quadrupole interaction is introduced by the index of refraction, while the geometry is determined by the flat metric, proportional to (3). Can we associate a wave function to such a process?
For the quadrupole interaction we have a wave function whose eikonal and amplitude are approximately given by
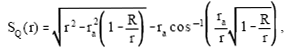 | (34) |
and
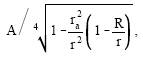 | (35) |
respectively, since R/r is a very small quantity. The square of the amplitude, (35), is an intensity which measures the ‘geometric divergence’ of the wave field[17]. The larger it is, the more the rays in the neighborhood of some fixed ray will diverge from each other. In the absence of the quadrupole interaction the geometric divergence becomes infinite on the caustic r = ra, which is the case of the ordinary Bessel function. In the presence of the quadrupole term, the geometric divergence of the ray field becomes infinite at a distance smaller than ra. The equation of the trajectory,
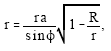 |
shows that the trajectory becomes infinite as φ→0 and π, while the distance of closest approach r0 is less than the caustic radius ra. Consequently, as the result of the quadrupole interaction the distance from the scattering center to the caustic has been reduced. In the limit as r→r0, the form of the wave function (4) is no longer valid and a uniform asymptotic expansion of the Bessel function can be given in terms of Airy functions[18].
The differential cross section of the quadrupole interaction is:
which displays the characteristic scattering property of the cross section to approach infinity as the angle of deflection approaches zero. However, since the rest energy is involved, there will be no rapid decrease of θ with the kinetic energy, as is usually the case in particle scattering.
THE PERIHELION SHIFT
Thus far we have treated open trajectories A<0. In the case of Mercury, we are dealing with a closed orbit and hence negative total energy A>0, which is not exactly elliptical due to the advance of the perihelion. This precession amounts to 43" in a century and was known to astronomers as early as 1860. However, its explanation had to await the general theory of relativity in 1915.
Taking into account both the gravitational potential and the quadrupole interaction, the index of refraction is [vid. (30) with c1 = 0 and c2 = 1 ]
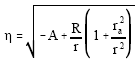 |
In the unperturbed state, where, the quadrupole interaction is absent, the gravitational potential must be large enough so that the eccentricity is real [vid.(17)]. The eikonal is
 | (36) |
A closed trajectory will result from a dynamic balance between gravitational and centrifugal forces.
In the presence of the quadrupole interaction, the angular momentum will exist only for radii r>3/2R. Introducing this fact into (36) through the transformation, r+3/2R = r’ and retaining terms that are at most quadratic in the Schwarzschild radius, give
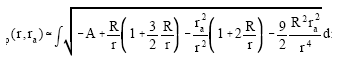 |
where for brevity we have dropped the prime on r.
Expanding the integrand in powers of the small correction terms results in:
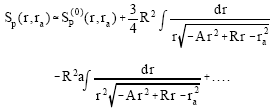 | (37) |
where, the unperturbed eikonal S(0)P(r,ra) is given by (16). The unperturbed orbit, -S P(0)/∂ra = φ is given by the ellipse (19) since ∈<1.
The change in S(0)P over one complete orbit is:
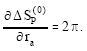 |
As r goes through one libration, the true anomaly φ increases by 2π and there is no perihelion advance. However, taking into consideration the first order correction term in (37), which can be written as
 |
and differentiating it with respect to ra, give the first order correction term:
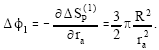 | (38) |
Introducing the semi-latus rectum (18) results in:
| (39) |
which is the general relativistic result for the perihelion shift. For Mercury, the rotation of the perihelion per revolution amounts to 0.104". The dimensionless energy constant A = 2.59x10-8 and the mean motion ω = rac/ab = 2cA3/2/R = 8.34x10-7 s-1, where we have reinstated the speed of light c and ![]() is the semi-minor axis. The period of the motion of Mercury is T = 2π/ω = 87.25 days, which is close to the actual value of 88 days. The frequency of rotation of the perihelion will be Δω = ωΔφ1 = 4.25x10-13 s-1.
is the semi-minor axis. The period of the motion of Mercury is T = 2π/ω = 87.25 days, which is close to the actual value of 88 days. The frequency of rotation of the perihelion will be Δω = ωΔφ1 = 4.25x10-13 s-1.
There are five experimental confirmations of general relativity: time delay in radar sounding, deflection of light, perihelion advance, spectral shift and the geodesic effect. We have shown that three of these effects can be treated as diffraction phenomena on the basis of Fermat’s principle and the modification of the phase of a Bessel function in the short-wavelength limit. The spectral shift can also be derived from energy conservation by assuming that a photon’s energy has both inertial and gravitational mass. This depends in an essential way on the equivalence principle and not upon general relativity.








