Research Article
A Class of Explicit Fourth Order Method with Phase Lag of Order Six for Second Order Initial Value Problems
Department of Computer Science, International Islamic University, H- I C), Islamabad, Pakistan
A class of two-step hybrid methods for the numerical integration of second order initial value problem
| (1) |
is defined in the following. Let h>0 denote the stepsize tn = t0+nh, h = 0,1,2,… and set yn = y(tn), fn = f(tn,yn).
We consider the method of the form
| (2) |
| (3) |
| (4) |
| (5) |
where:
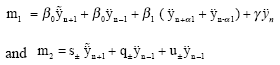 |
The methods are fourth order accurate if satisfy the following conditions.
| i) | |
| ii) | |
| iii) | |
| iv) | |
| v) | |
| vi) | |
| vii) | |
| viii) | |
| ix) | |
| x) | |
xi) | |
xii) | |
| xiii) | A±+B±+C± = 1 |
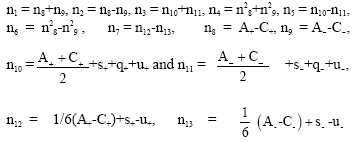 |
and n14 = s++s+u++u– and the local truncation error is
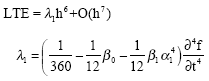 | (6) |
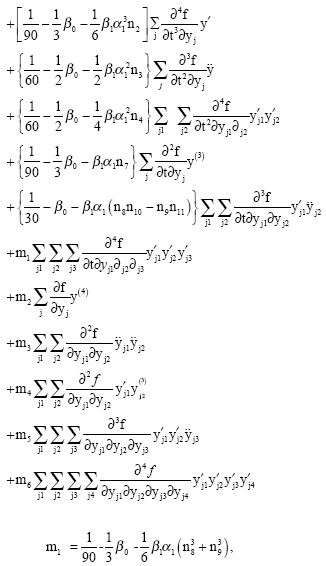 |
 |
Further from condition (ii) either β1 = 0 or A++A–-C+-C– = 0. Also from condition (vii) either β1 = 0 or α1 = 0 or A++A–-C+-C– = 0. We consider the case where β1 = 0 and β1≠0.
Case 1: If β1 = 0 then from condition (iii) β0 = 1/12 and from condition (i) γ = 5/6. Then the local truncation error from (6) becomes
| (7) |
Case 2: If β1≠ 0 then either α1 = 0 or α1 ≠ 0.
(a) If α1 = 0 then we have from the conditions
| (8) |
and the LTE becomes
| (9) |
where, ![]() and
and ![]()
Observe that Chawla and Rao[1] method is of this class. They choose the parameters as
| (10) |
and
LTE
| (11) |
(b) If α1≠0 then fourth order conditions becomes
 |
and the local truncation error becomes
| (12) |
where
 |
P-Stability: Lambert and Watson[2] have given the definition of P-stability
To analyses the stability properties of the method, we apply the method (2), (3), (4) to the scalar test equation:
| (13) |
We obtain the stability polynomial
 | (14) |
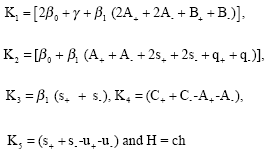 |
Equation (14) is a difference equation of the form[3]
| (15) |
where:
When we apply the fourth order condition then the stability polynomial is of the form![]() where,
where,![]()
Making the Routh-Herwitz transformation ![]() (15) becomes
(15) becomes ![]()
Thus, the necessary and sufficient conditions for P-stability are![]()
Since ![]() then the condition becomes
then the condition becomes ![]() and the necessary and sufficient conditions for P-stability are
and the necessary and sufficient conditions for P-stability are ![]() and
and
| (16) |
where:
| (17) |
and
| (18) |
Condition (18) is satisfied iff![]()
![]() Thus the methods are P-stable if satisfy the condition (17) and (18) with
Thus the methods are P-stable if satisfy the condition (17) and (18) with![]()
Phase LAG: When the method (2), (3) and (4) is applied to the scalar equation (13), we have the recurrence relation[4]:
Substituting ![]() we have
we have
on expansion of and , we have the form
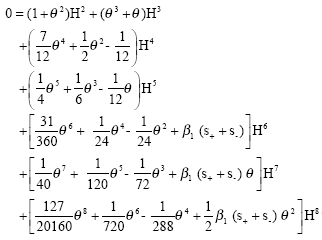 | (19) |
Let ![]() Substitutes in (19) and then comparing the coefficients of Hj, j = 2, 3,4,5,6 to zero, we get
Substitutes in (19) and then comparing the coefficients of Hj, j = 2, 3,4,5,6 to zero, we get
Thus we have
If ![]() which is greater than 1/576 (P-stability condition), we may write
which is greater than 1/576 (P-stability condition), we may write ![]() and on substituting in (19) and then comparing the coefficients of H7 and H8 to zero, we get η5 = 0 and
and on substituting in (19) and then comparing the coefficients of H7 and H8 to zero, we get η5 = 0 and ![]()
Thus the quantity b-1 in the definition of phase lag is
| (20) |
PARTICULAR METHODS
Case 1: β1 ≠ 0 and α1 = 0 Observe that Chawla and Rao[1] method is of this class with parameters.
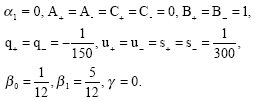 | (21) |
In this case ![]() satisfy the P-stability condition and also phase Lag given by (20).
satisfy the P-stability condition and also phase Lag given by (20).
We choose the parameters in two different ways
| (a) | The points (tn-α1, yn-α1) and (tn+α1, yn+α1) are coincident and |
| (b) | |
| (a) | If the points (tn-α1, yn-α1) and (tn+α1, yn+α1) are coincident then |
| (22) |
then from (8)
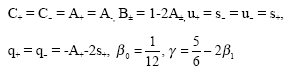 | (23) |
for P-stability we have ![]() and if we have
and if we have ![]() then the method has phase lag given by (20). Thus we take
then the method has phase lag given by (20). Thus we take ![]() for P-stable method. We choose β1 = 1, then s+ = 1/720. Also let A+ = 1/2.
for P-stable method. We choose β1 = 1, then s+ = 1/720. Also let A+ = 1/2.
| (b) | For |
| (24) |
then from (8)
| (25) |
and for P-stable with phase lag given by (20), we must have ![]() . Thus we choose β1 = 1, then s+ = 1/360. Also let A+ = 1/2
. Thus we choose β1 = 1, then s+ = 1/360. Also let A+ = 1/2
Also we test the method with A+ = 0 and β1 = 1/3, then s+ = 1/120. The local truncation error for all these method is
| (26) |
Case 2: If β1 ≠ 0 and α1 ≠ 0, we have chosen the method for α1 = 1. In this case ![]() Then
Then
| (27) |
then from (11), we have
| (28) |
For P-stable method with phase lag of order eight given by (20), we must have ![]() or in this case,
or in this case, ![]() We choose β1 = 1 and A+ = 1/2, then,
We choose β1 = 1 and A+ = 1/2, then, ![]() For these methods, LTE is given by (26).
For these methods, LTE is given by (26).
Methods for different examples were tested. The methods are given below.
The methods derived above and used for companion purpose in next section.
M 1: Given by equations (22) and (23) with parameters β1 = 1, S+ = 1/720 and A+ = 1/2
M 2: Given by equations (24) and (25) with parameters β1 = 1, S+ = 1/360 and A+ = 1/2
M 3: Given by equations (24) and (25) with parameters β1 = 1/3, S+ = 1/120 and A+ = 0
M 4: Given by equations (27) and (28) with parameters β1 = 1, S+ = 1/360 and A+ = 1/2
M 5: Given by equations (21).
NUMERICAL ILLUSTRATION
We have tried a number of explicit scalar (nonstiff) test problems of the form (1). They give similar results and so we restrict our attention to one oscillatory example.
| Example 1: |
This is a pure oscillation problem whose solution has maximum amplitude unity and period approximately six. We have calculated error as |Error at t = 6|
In Table 1-3 we present the following statistics:
1) Number of evaluation of the differential equation right hand side f, FCN;
2) Number of steps overall, NOST;
3) Number of successful steps to complete the integration, NSST;
4) Number of steps where the stepsize is changes, NCST;
5) Number of failed steps, NFST;
6) Number of steps on which the iteration diverged, NDIV;
7) Number of steps where the stepsize is halved, NHST;
| Table 1: | Comparison of the method for example 1 with Tol = 10-2 |
 | |
| Table 2: | Comparison of the method for example 1 with Tol = 10-4 |
 | |
| Table 3: | Comparison of the method for example 1 with with Tol = 10-6 |
 | |
Next we consider example for system, where we use a test problem a moderately stiff system of two equations.
| Example 2: |
For this example we have deliberately introduced coupling from the stiff (linear) equation to the nonstiff (nonlinear) equation. For this example again we have calculated error as ||Error at t = 6||∞.
| Table 4: | Comparison of the method for example 2 with with Tol = 10-2 |
 | |
| Table 5: | Comparison of the method for example 2 with with Tol = 10-4 |
 | |
| Table 6: | Comparison of the method for example 2 with with Tol = 10-6 |
 | |
Example 3: Consider the almost periodic linear problem studied by Stiefel and Bettis[5].
![]() with analytic solution.
with analytic solution.
Z(t) = cost+0.0005tsint+i(sin t-0.0005t cost).
This solution represents motion on a perturbed circular orbit with the distance from the origin |Z(t)|. We have computed solution to this problem using our fourth order method. We use the system
Where, Z = u+iv. After computing u and v, we have calculated |Z| at t = 40π with stepsize h = π/4. Result are presented in Table 7-9 and comparison of approximation in Table 10.
| Table 7: | Comparison of the method for example 3 with with Tol = 10-2 |
 | |
| Table 8: | Comparison of the method for example 3 with with Tol = 10-4 |
 | |
| Table 9: | Comparison of the method for example 3 with with Tol = 10-6 |
 | |
| Table 10: | Comparison of the approximation produced at Z=40π with h=π/4 initially.Exact value is Z(40π)=1.0019720 |
 | |