M. Benyettou
Not Available
S. Chouraqui
Not Available
A. Bouadi
Not Available
ABSTRACT
The problems met during the coalescence of fluid drops (liquid or gaz) in chemical reactors or other, brought ourself to study the dynamics of drops put on an inclined solid plane. The first part of this study is consecrated to characterize the fluid-solid interfaces by a certain number of parameters which could be introduce in the equations of topic. The spreading of the drops then described. In the second part, this study resolve non linear partial differential equations of second order giving the difference profiles of the sessible drop on the horizontal plan and then tilted. The crawling of the drop of the tilted plan is described. A valuing of critical volume of the drop in function of the angle of slant is expressed.
PDF Abstract XML References Citation
How to cite this article
M. Benyettou, S. Chouraqui and A. Bouadi, 2005. Drop Behavior on an Inclined Solid Plane. Journal of Applied Sciences, 5: 1690-1691.
DOI: 10.3923/jas.2005.1690.1691
URL: https://scialert.net/abstract/?doi=jas.2005.1690.1691
DOI: 10.3923/jas.2005.1690.1691
URL: https://scialert.net/abstract/?doi=jas.2005.1690.1691
Problem posed: The two following equations present the profil of the water drop on an inclined plane (Fig. 1)[1,2]
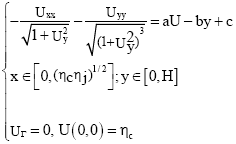 | (1) |
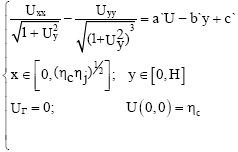 | (2) |
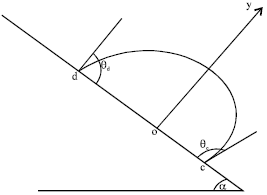 | |
| Fig. 1: | Inclined drop |
| α : | Inclined angle. |
| θc: | Advanced contact angle. |
| θd: | Retired contact angle. |
| ηc: | Distance of point o to c. |
| ηd: | Distance of point o to d. |
Resolution of the problem: Implicit finit differences methods were choosed to resolve the problem posed[3-5].
Discretisation of the domain:
We adopt the net of points of the domain (Fig. 2); more informations:
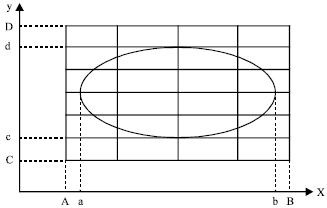 | |
| Fig. 2: | Discretisation of the domain |
Nx, Ny two integers which determin the number of [A, B], [C, D], respectively.
U(x,y) function of two independant variables, suffisuntly differenciables.
 | (3) |
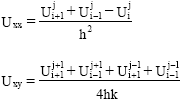 |
With = ![]()
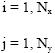 |
The resolution of the Eq. (1) is realised by the Newton-Raphson[6] (Fig. 3 and 4).
Then, we define ![]() by:
by:
| (4) |
This converge to a solution of (1-1) with:
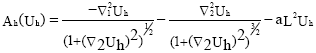 | (5) |
With:
 |
The same operation to the Eq. (1-2). except:
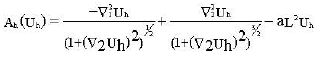 |
 | |
| Fig. 3: | Associed to the test 4 |
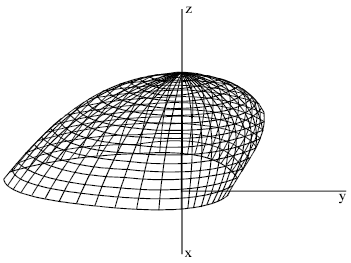 | |
| Fig. 4: | The test 4 after the transformation by the procedure |








